S H M problem Time Period

JEE Main 2015 Guidance › Mechanics questions › S H M problem Time Period

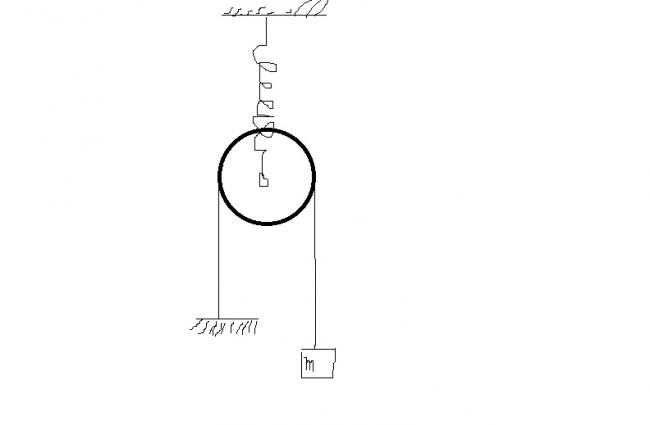
In the given figure, the spring has spring constant k . The pulley is light and smooth , the spring and the string are light. The suspended block has a mass m. If the block is slightly displaced from its equilibrium position and then released.Find the time period of its vertical oscillation.

#Physics #Mechanics

UP 0 DOWN 0 0 3
Post on FacebookPost anonymously?

3 Answers

23

qwerty ·2011-04-11 03:58:01

just find by how much does the spring stretches when you displace the mass by x

UP 0 DOWN 0
Post on FacebookPost anonymously?

30

Ashish Kothari ·2011-04-11 05:19:43

Let the spring be stretched by x₀ and the block be displaced by x.

If the restoring force on the block be F_r.

Note, 2x₀=x ... (i)

2F_r = kx₀

x₀ = 2F_rk

Put in (i),

4F_rk=x

4mÏ‰²x = kx

Ï‰ = 12âˆš(k/m)

Time period = 4\pi \sqrt{\frac{m}{k}}

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

Pratikshit Singh ·2011-04-11 07:18:53

Ohh thanks Ashish i did everything right except equating 2f_r=kx_o i equated
f_r=kx_o

UP 0 DOWN 0
Post on FacebookPost anonymously?

Your Answer

Basic Integral Calculus Operators Symbols Matrix Cases

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω