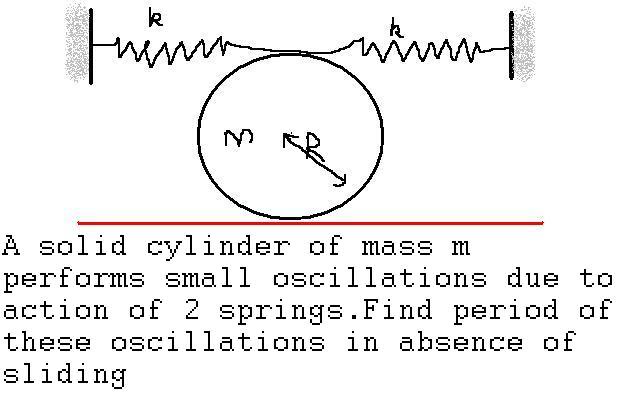
1we can conservve energy about point of contact since no slipping there..
so
U = 1/2 k x2 + 1/2 k x2 + 1/2 I ω2
= 1/2 k x2 + 1/2 k x2 + 1/2 (mR2 + 2/5 R2)ω2
diffrentiating both side,
0 = 2kx v + 7/5m v a
=> a = -(10k/7m) x
so, ω2 = (10k/7m)
bus [1]
1oh shit.
it was a solid 'cylinder'... n i constantly read it solid 'sphere'...
dats y told diptosh n all incorrect.. [2] [2] [2]
I AM TOOOOO SORRY TO U ALL N MOST IMPORATNTLY MYSELF (for not able to materialise successfully my N-Y resolution [2] [2] .... bhaiya i will 'try' harder to avoid these... [2])
62sky, your mistake is that you have taken I corresponding to a sphere.. here it is a cyllinder...
Kep in mind that these misakes will kill all ur preparations... You have to not make these mistakes.... other mistakes are allowed...
62the total energy of the system is constant and then find its derivative..
E=1/2k(2x)2+1/2k(2x)2+1/2mv2+1/2 Icm(v/r)2
I=1/2Mr2
v=dx/dt
E=k(2x)2 + 3/4mv2
E=k(2x)2 + 3/4m (dx/dt)2
now take dE/dt=0
8kx(dx/dt)+3/2m(dx/dt) d2x/dt2 = 0
8kx+3/2md2x/dt2=0
d2x/dt2=-16k/3m x
hence 2pi √3m/16k
pi √3m/4k
1energy eqn ??
i am correct..
i have taken for point of contact..
u took it for com.
3Hint:
the total energy of the system is constant and then find its derivative..
E=1/2k(2x)2+1/2k(2x)2+1/2mv2c+1/Icm(vc/r)2
and x is the distance moved by com at a particular instant
62it is on the top and i think this is from Irodov.. a standard problem which is not very difficult...
I think the expression sankara gave is correct.. you just need to do a bit more to that
ie find the relation between v and x!
