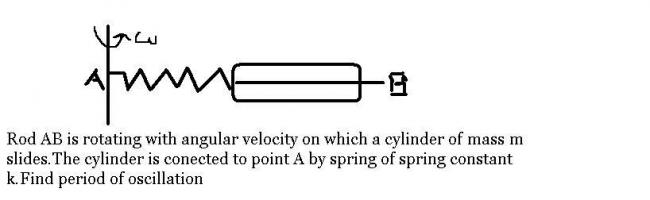
i think tushar ur wrong as........ u hv to express iin terms of @
Practice questions for SHM...
Level=easy
Q1 Dtermine the natural frequency of vibration of 100N disc.Assume it does not slip on inclined surface
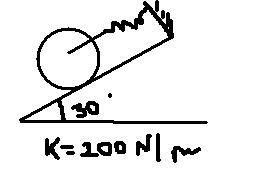
Q2The disc has weight=100N and rols without slipping on horz surface as it oscillates about eq position.If disc is displaced by rolling counterclockwise 0.4 rad,determine eqn which describes oscillatory motion
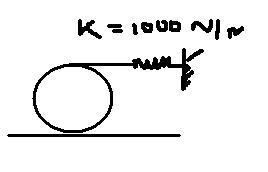
Q3 An object is suspended from a spring exhibits oscillations of period T.Now the spring is cut in half and two halves are used to support the smae object.Show that new time period is T/2
Q4 A particle performs SHM in straight line.In first round starting form rest,it travels distance a and next second it travels distance b in smae direction.Find amplitude of SHM
-
UP 0 DOWN 0 0 22

22 Answers
kk dude first sum easy one one simple doubt lets oslv ehte sum by... force method
we are assuming mgsin@=kx why not mgsin@+f=kx or mgsin@=kx +f as it is in equilibrium
Q4level easy.........
Particle atarts from xtreme post.(from rest)
x=Acoswt (t=0,x=a)
A-a=Acosw........(given).....(1)
A-(a+b)=Acosw......(2)
solving 1,2
4Aa-aA-bA=2a2
A=2a2/(3a-b)
Q4 level easy.....what is 'first round'?Is it 1 oscillation.........
Or is it first 'second'.........
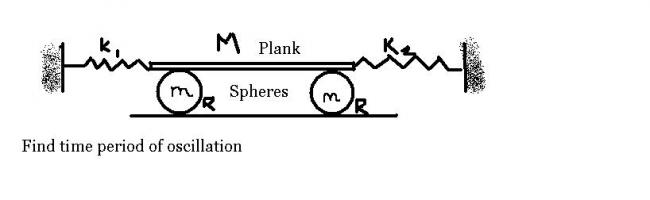
Q-10level difficult
(Assumption:spheres are rolling and there is enough friction for rolling,without which the rod and spheres cannot be in equilibrium.)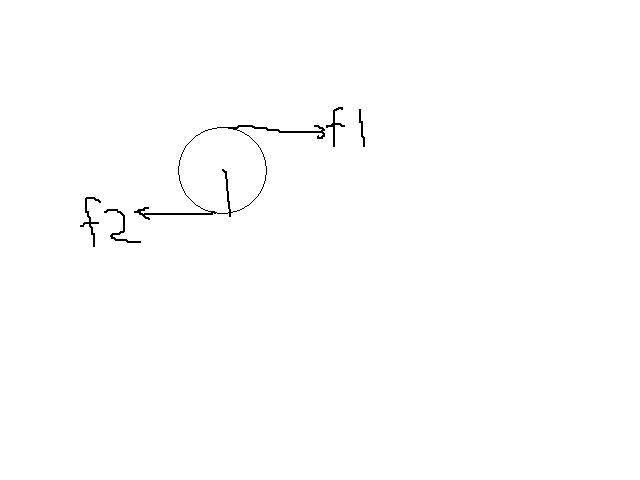
[The force on the left side of the rod is (k1+k2)x]
f2 is the friction due to the floor on the spheres.
suppse 'a' is the acceleration of the plank in the horizontal direct.
Acc. of COM of spheres=a/2.....(rolling condition)
f1-f2=ma/2...........................(1)
(f1+f2)R=2mR2a/10
f1+f2=ma/5...............(2)
so,2f1=0.7ma.
now, from FBD of rod,
Net horizontal force=(k1+k2)x-2f1=Ma
Ma=(k1+k2)x-0.7ma
thus we get time period as
2\Pi \sqrt{}(M+0.7m)/(k1+k2)
this is my solution
....... pls correct it if it is wrong
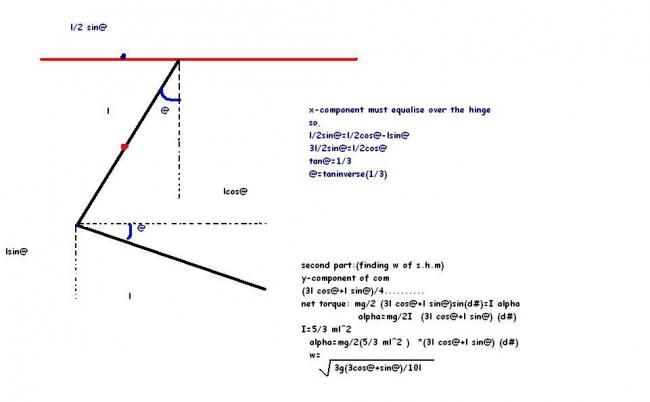
first we cant use force method in these questions as the hinge exerts a force
now ..............
in equillibrium
kl/4=Mg3l/4+mgl/2
no need to calculate l
now let the rod be displaced by an angle@ then tan@=x/3l/4
therefore x=3l@/4.......
now we can continue tushars method...................
Q3 level easy.
spring is cut into halves.
so new spring constants=2k,2k.
Equivalent spring constant=2k+2k=4k
T1/T2=√4k/k=2
T2=T1/2.
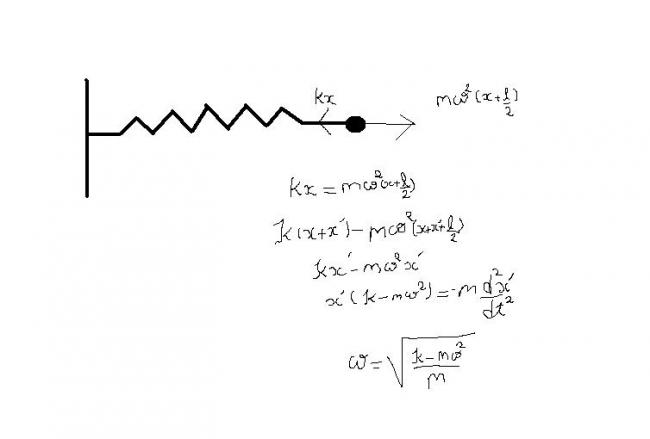
Ans1) In =lbm ,mg sin θ = k x0
When displaced by x,
E = (1/2)mv2 + (1/2) Iw2 + (1/2)k(x+x0)2 - mg sin θ
Since E= constant (Total Mechanical energy remains const in S.H.M)
Therefore, put dE / dt =0
0 = mv (dv/dt) + Iw (dw/dt) + k(x+xo) dx/dt - (mg sin θ) dx/dt
Substituting, dv/dt = a, w=v/R, I = (1/2)w R2
d w /dt = α = a/R , dx/dt = v and kx0 = mg sin θ
we get, 3ma = -2kx
Therefore, f = 1/2∩ √(a/x) = 1/2∩ √2k/3m [Taking mod |a/x|]
On substituting the values, we get, f = 1/2∩ √(4/3 x 9.8) = 0.56 Hz
The first and second ques of LEVEL = EASY can be easily solved by the concept of energy mrthod
Since total mechanical energy of the spring block system is const we can diff it w.r.t t and put equals to zero.
LEVEL = MEDIUM
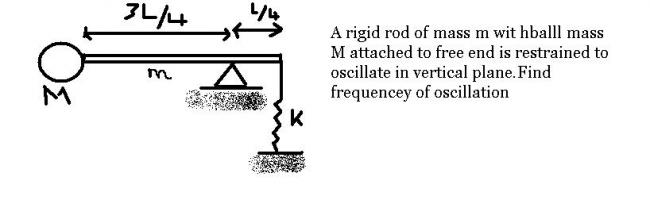
Ans2) At =lbm posn, deformation of the string x0,
kx0 ( l / 4) = Mg ( 3/4 l ) + mg (l/4)
When the rod is furhter rotated through an angle @ frm an =lbm posn,
the restoring torque is
= - [ (x + x0 ) l/4 cos @ - Mg (3/4 l ) cos @ ] - mg (l/4) cos@
= - [ (x + x0 ) l/4 - Mg (3/4 l ) - mg (l/4)] cos@
Now for small @ , cos@ =1 (approx)
Therefore, torque = - k l / 4x
I α =( -k l / 4x ) @ [bcoz torque = I α ]
Where I = M (3/4 l) 2 + ml2 /12 + m (l/4) 2
Therefore, f = 1/ 2∩ √[3 k / (27M +7m])
looks like No one is intrested in solving ques at tiit these days....