no.....
ans. is = mm+M H cot( theta)
A smooth wedge of mass M with a small block of mass m at the
highest point of its inclined surface is released from rest on a fixed
smooth horizontal surface, as shown. Initially block is at rest with respect to the wedge surface and the angle of inclination
of the inclined surface with respect to the horizontal is theta. Find distance traveled by the wedge with respect to the horizontal
surface when the block reaches the lowermost point of the
inclined part of the wedge.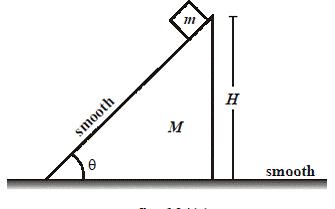
plz solve it by newton's law...i hv solved it by centre of mass...nd got d ans...but i ain't getting the same ans. by newton's law.....
The wedge moves only due to the sine component of N provided by the block...
assume that the accn of wedge is 'a'(right) and that of block is 'b' (down the plane wrt wedge)
Now find out the absolute accn of block if u solve from ground frame..or add a pseudo force if u solve wrt wedge.
Let \: a_{0}\: be \: the \: acc.\: of \: the \: block.
Let \: a\: be \: the \: acc.\: of \: the \: wedge.
Therefore,
ma_{0}= \: mgsin\theta \: + macos\theta \:....(1)
N=mgcos\theta \: - \:masin\theta \: ..... \:(2)
Nsin\theta = Ma \: .... (3)
Solving 2 and 3,
a = \frac{mgsin\theta cos\theta }{M + msin^{2}\theta }
Using this to solve 1,
a_{0}= \frac{gsin\theta (M+m)}{M+msin^{2}\theta }
Now, the length of the inclined part = \frac{H}{sin\theta }
Hence, displacement of block,
\frac{H}{sin\theta } = \frac{1}{2}\frac{gsin\theta (M+m) }{(M + msin^{2}\theta )} t^{2}
\Rightarrow t^{2} = \frac{2H(M+msin^{2}\theta )}{gsin^{2}\theta (M+m)}
Therefore, distance travelled by wedge,
D = \frac{1}{2}\frac{mgsin\theta cos\theta}{(M+msin^{2}\theta)}t^{2}
D = \frac{m}{M+m}Hcot\theta [Ans.]
:)
I hope this will help a little more.
The FBDs of the wedge and the block.
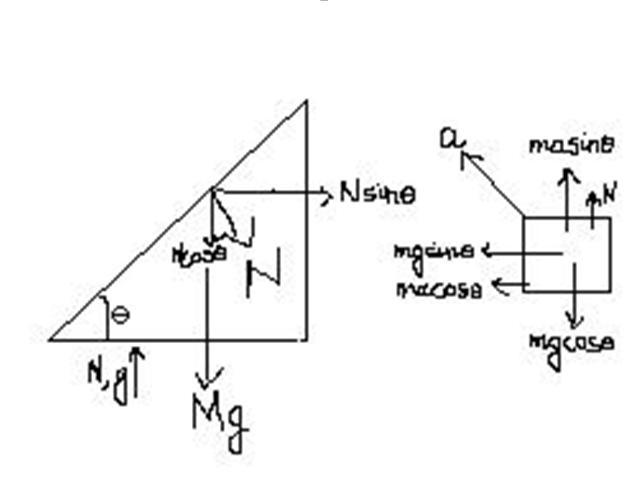
@ ashish_k04.....thnx for posting diagram....but to be honest there wasn't any need for that.....i too did d same thing but made calculation mistake in calculating a :) ............
but this problem is really good example to show how powerful center of mass concept is.......using COM just a single eq. will give the desired result.................