1some part of the motion may be related to projectile motion
8 Answers
1Firstly i believe problem "overclaims"(i think problem needs some correction)!
(hypothesis of problem just means that coefficient of friction=tan@,@=angle of incline....i.e. net acceleration down the hill is 0)
Lets Take X-axis in "horizontal" direction and Y-axis down the hill!
X-axis situation
ux(initial velocity)=1
ax(acceleration)=-tan@g
so Vx=1- tan@g*t
Y-axis situation
uy=0
ay=0
so vy=0
so speed would always be along horizontal and finally would become zero!
21Vivek, i have the pdf with 89 problems only..leave about solution..i don't even have the answer
21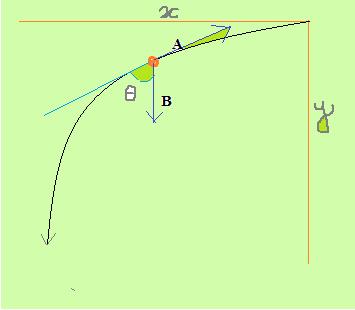
Clearly the friction co-efficient is tan(a).The force A(due to friction) is mgsin(a) and B is also mgsin(a).
The velocity along x and y direction is Vx and Vy.
There resultant makes angle theta with Vx. where theta is the angle as shown in figure.
(to be continued..)
1@vivek
thanks for the solution...but i stll am confused....Clearly even the solution say that there is no acceleration down the plane!further boy is pushed horizontally...i.e. to say his initial velocity down the plane is zero!so final velocity down the plane is zero of course.....where's the flaw?
21If we replace mgsin(a) by k ,then force along x direction = \frac{dv_{x}}{dt} = -ksin\theta____(1) and force along y-direction is \frac{dv_{y}}{dt} = k-kcos\theta____(2)
From the figure in post 6,we see \frac{dy}{dx}= cot\theta\Leftrightarrow v_{y}= v_{x}cot\theta
differentiating \frac{dv_{y}}{dt}= \frac{dv_{x}}{dt}cot\theta- v_{x}cosec^2\theta\frac{d\theta}{dt}
plugging equation (1) and (2) in this relation ,we get k= - v_{x}cosec^2\theta\frac{d\theta}{dt}
combining this ,with equation (1) we get
\frac{dv_{x}}{v_{x}}= cosec\theta d\theta
on integrating with initial velocity(x-direction) 1m/s and final horizontal velocity Vx and initially \theta= \frac{\Pi }{2} and finally equal to \omega (Let) as limits of integration
we get,ln(V_{x}) = ln(tan\frac{\omega }{2})
or V_{x} = tan\frac{\omega }{2}
If the resultant velocity is V, then V = \frac{V_{x}}{sin\omega}\; =\; \frac{1}{(1+ cos\omega)}
we have got V as a function of the angle \omega
when \omega\rightarrow 0 ,V= \frac{1}{2}m/s