Q9 Accelration
Q13 On the lamina[1][1]
Yesterday Philip was frustrated at the lack of gud problems...I am posting some for everyones practice..........2009 aspirants should solve them and put up solutions here for 2010 students to learn.............
Some might be easy.......but all are conceptual[1][1].....
Q1 A uniform rod of length 2a and mass m is rotating in horz plane about a smooth fixed pivot through the centre of rod with a constant angular velocity w rad/s.A particle of same mass moving with speed aw/4 opposite t orod strikes one end of the rod perpendicular to it.If e=1/2,calculate angular velocity of rod immediately after collision.
If anyone has problem with my initiative he/she is free to express his/her views...........i wont feel bad at all and i will stop this work at that moment only..[1][1][1][1]
q9 ... woh kya hai...accn ya velocity??????????
q 13 .. that boy walks on the lamina or around the lamina ..... ???????
and 1 last thing ... the water is fallin vertically on the buckets??????
whom are u telling that????????[7]
ur ans is wrong..........ans is 3ω
u can assume it vertical..........i found it yesterday only..........i still have to solve it.....busy with boards[3][3]
IM QUITE SURE OF MAH METHOD ......... MUSTA BEEN SUM CALC. MISTAKE .......
AND I WAS TELLIN DAT TO SUM GUY WHO JUST DEL. HIS POST......
okk........recheck it......cant do it now......got to go.......sorry.....[2][2]
okie the bucket answer 12 ....
since no torque .... assumin vertical fall of water......
ang mom conserved ....
I W0 = (I + mtr2)W .....mt = mass of water out in t sec .........
W = IW0/(I + mtr2)
dθ/dt = IW0/(I + mtr2)
θ = IW0ln(I + mtr2/I) / mr2 ..........
THE 10 1 .... IM ASSUMIN AT THE END OF THE TURN THE SURFACE IS NEARLY FLAT!!!!!
SO v =√2gnh
so accn = v2/R = 2gnh/R ....................[NO VERTICAL ACCN.....]
IM ASSUMIN SURFACE TO BE FLAT[horizontal] NEAR END OF CURVE FOR SIMPLICITY ..........
IN 13 WALA COM IS IN SAME POS. RITE [ASSUMIN MAN DOSNT WALK BY VIRTUE OF FRICTION [PRACTICALLY IMPOSSIBLY ....[HEHEH]]
BUT AR U SURE HE WALKS ON DA LAMINA....
CUZ WHEN HES AT POSITION O .......
THEREZ NO WAY U CAN KEEP THE COM LIKE HOW IT WAS INITIALLY............
yup.......correcto................Q12 answer is correct......
btw why only sharman is trying these questions????Are u all not giving JEE??????[12][7]
Very easy as compared to all the problems we have done before.........
Q14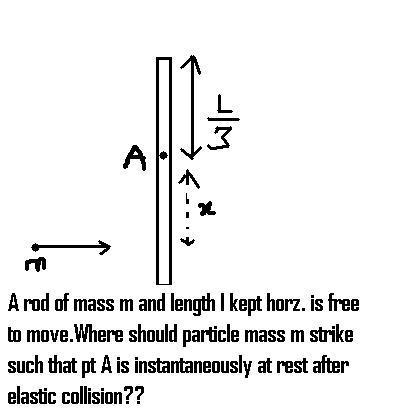
And plzzzzzzz guys solve the remaining ones............these are very good problems.............If no one is taking interest then i should close this thread probably........[2][2]
Q15 A uniform stick of length L and mass M hinged at one end is released from rest at angle θo with the vertical Find the force which hinge exerts along the stick and perpendicular to it at an angle θ with vertical.
I am completing the quota....so dont mind it that I am posting so many in one go.......
keep trying.......
Q16 A cylinder of mass m is kept on edge of plank of mass 2m and length 12 m,which in turn is kept on smooth ground.μ between plank and cylinder is 0.1 .The cylinder is given an impulse which imparts 7m/s velocity to cylinder but no angular velocity.Find time after which cylinder fallls off plank
Eureka, u forgot yourself.......U TOO ARE A PHYSICS GENIUS
I still remember 2 months ago when i used to visit the toilet each time i see one of your physics questions!!!
he he .....me a physics genius.....thanx for compliments.........but these all questions are for u all ...........for ur revision........and no one attampts them even except sharman ..............
I feel bad then........[2][2]
ANd ya i remember those peculiar things 2 months back.......u even started a thread!!!!!!!![3][3]
Q 14
WARNING: IGNORE THIS POST CUZ THE QUESTION HAS MENTIONED ELASTIC COLLISION WHILE IVE THOT INELASTIC COLLISION
Conserving linear momentum...
mv = 2mVcom
==> Vcom = v/2 .... (i)
I am taking R as the dist. from the COM of the stick where the ball collides. After collision the COM shifts R/2 downwards.
So, new MI = [mL2/12 + m(R/2)2] + m(R/2)2
Conserving angular momentum,
mvR/2 = Iω
==> ω = mvR/2I ... (ii)
Now point A is at a distance L/6 + R/2 from new COM. For it to remain at rest,
ω(L/6 + R/2) = Vcom
Putting the value of ω from (ii) and Vcom from (i)
we have R = L/2.
So x is 2L/3 (assuming x is dist from end)