1yayyyyyyyyyyyyyyyyyyyyyyyyyy!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
lemme celebrate for 5 mins!!!!!!!!!!1
then i will post the ans in next 5 mins .. [3] [3]
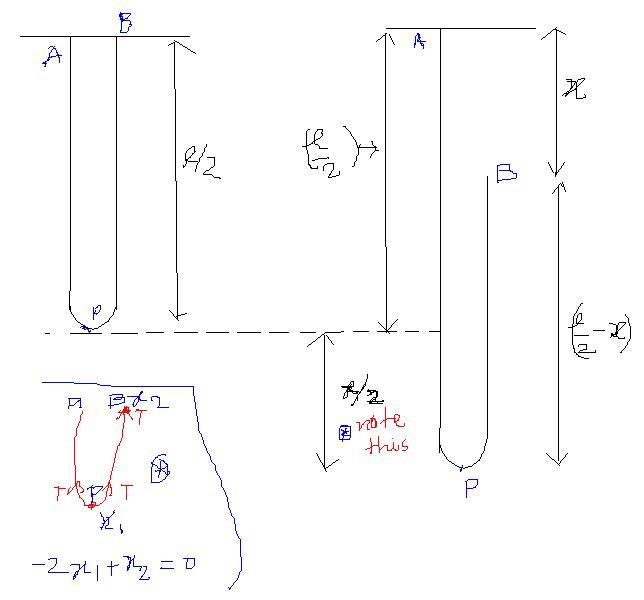
A uniform chain of length L and mass M is hanging vertically from its ends A and B which are close together.At a given instant the ened B is released.Find the tension at A when B has fallen a distance x(<l)
-
UP 0 DOWN 0 3 52
52 Answers
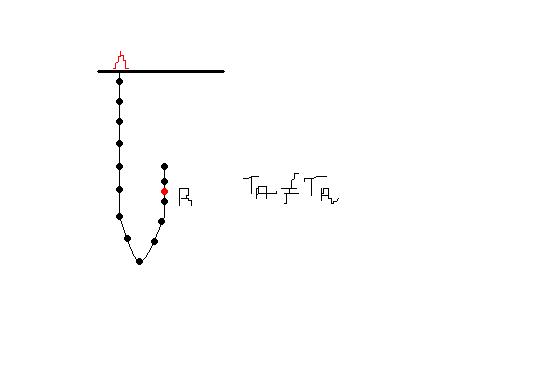
3please correct me if i was wrong with my fbd
the orange dot shows the location of the cm of the hanging part
and the small black dots shows the continous distribution of differential mass element.
1
3hey sky wont the tension will be different at diff points since it is an uniform chain
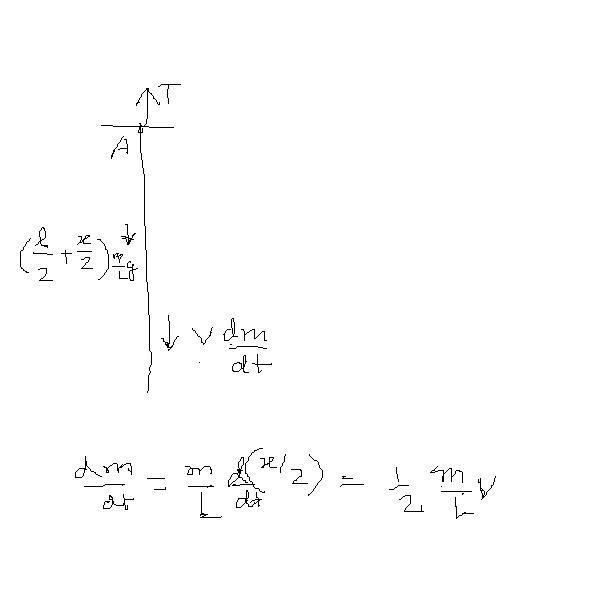
1let at some time 't',
B falls by a distance 'x'.
vel of point B = √2gx. (free fall)
now, ocnsiedr the free body diag of right part...
mg(l/2 - x) downwards n m/L(v2) upwards.
now consider the free body diag of left part ..
T upwards, mg(L/2+x/2)/L downwards and 1/2vdm/dt.
vdm/dt = m/L (v2)
so, T=mgx/L + mg(L/2 + x/2) = mg/2 (3x/L +1) .
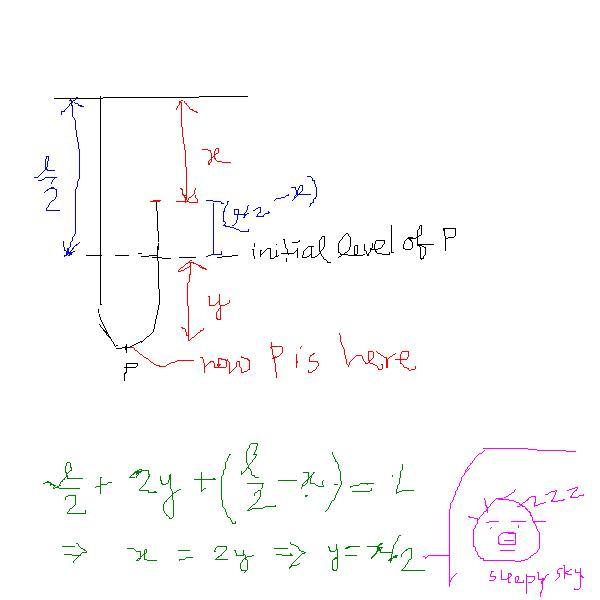
1see, if the tip B comes down x dist, the lowermost point P comes dwn by x/2 ... jus think physicaly........
1ok i am sorry to draw that diagram(the constraint diag only ).........
its a wrong interpretation...
actually i thot that physically...
n thot how to explain... so drew it...
yup u are correct re... sorry i am wrong...
but are u convinced that dist moved by P
= 1/2 the dist moved by B ??
3actually i was confused sky . so far i had seen such relations when a
massless pulley is used ..
clueless sky abt that dist moved by P = 1/2 the dist moved by B
1see, B is moving x dist down,
there is a curve .... one min i will draw
3if there any other doubt in this question i will ask u tomorrow
will u come tomorrow..
3ok sky i got the constraint relation
and wat abt the tension. and how to include the variation of the tension along the string..............
1dun take tension about the tension within the string....
its not needed...
62no mg is not the right answer..
and btw this thread should nto be highlighted!