1
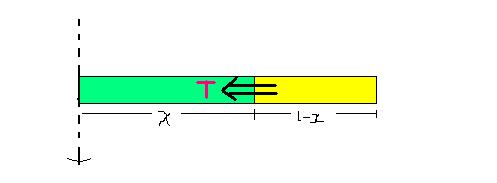
the latter part of the rod moves due to the tension(which i think u have missed)
So T = mrω2
or T = mL (L - x) . (x + L - x2) ω2
T = m2L (L2 - x2) ω2
which gives the ans...
A thin uniform metallic rod of length 0.5 m and radius 0.1 m rotates with an angular velocity 400rad/s in a horizontal plane about a vertical axis passing through one of its ends. Calculate the tension in the rod as a fucntion of distance from axis and the elongation of the rod.
The density of the material of the rod is 10^4 kg/m^3 and the Young's Modulus is 2 x 10^11N/m^2
I used integration and got T=8(pi) *106 * x2
But answer is 8(pi) *106 *[0.25- x2]
Please help with both.
-
UP 0 DOWN 0 0 1
1 Answers
1