13feelin much bttr got it...
but shudnt moment of inertia in ur 1st eqn be ml^2/3
i think u ve taken it as ml^2/6
The rod given in setup in fig1 is displaced slightly as shown in fig 2 find the time after which it will return to position in fig2
fig 1
_________________________________________________
fig 2
Take spring constant K, acc due to gravity as g, mass of rod m, length of rod L...
pulleys and string are ideal.
-
UP 0 DOWN 0 0 38
38 Answers
13
33First case when the rod is displaced left and motion from left extreme to mean and then from mean to left extreme(although after going right)....
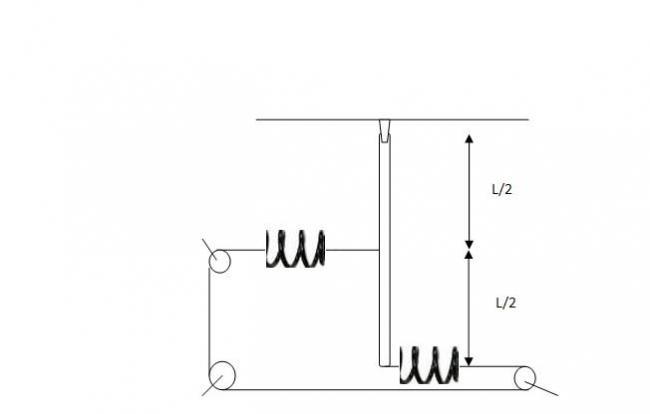
Then let θ be the angular displacement now the setup frees Lθ/2 of spring and pulls Lθ length of spring so net elongation in spring is is Lθ/2
,so
(1/2)(k/2)(Lθ/2)2+mg(1-cosθ)=(1/2)mL2/6ω2
now differenciate it and α comes out to be (3kL+12mg)θ/8
so T=2pi√8mL/(3kL+12mg)
now this motion is valid for motion frm mean position to left extreme and back to mean position so time taken is T/2.
____________________________________________________
Now for motion from mean position to right extreme and back to mean position....
Then let θ be the angular displacement now the setup frees Lθ of spring and pulls Lθ/2 length of spring so net it frees or say try to compress Lθ/2 of spring but due to string it can do so,so tension in string will become zero as it slacks.
so
in that case it will move under only gravity
so T2=2pi√(2l/3g)
now total time taken will be T/2+T2/2
i.e.
pi{√(8mL/(3kL+12mg))+√(2L/3g)}
calculation error may be there...
9superb q abishek especially the 2 part of motion
by the way why did u take mg(1-cosθ) in eq wen u assume θ as small u couldve safely neglected it
33Actually diffentiate it to get sinθ ant then write it θ :P
1hooray !! i got the answer in the first go without having to refer to any other post in this thread except the question one ....
why are these kind of q not posted in front of me [2][2]
by the way priyam ...
THIS WAS SERIOUSLY A BEAUTY..
AND TO QUOTE "It is a sort of one of its kind problem! "
[1][1]
33@deepanshu...
If x1 is elongation of first spring.. and x2 be of others..
Then as Tension is same in thread.. therfore..
Kx1=Kx2
so x1=x2..
Note: K is same for both...
13but y hv u considered 2 diff motions...
even thou both springs get strecthed at d same tym
33in second motion.. mean pos to right then mean...
String tries to compress spring but can it compress??
33:P
dekhte hain.... :P calculation mistake hua hoga.. koi badi baat nahi hai.. :P
33haan sayad...
1/2 multiply kar diye the ... lekin 1/2 alag se bhi lkih diye honge... :P
wo sab chalta hai.... type karne me... latex nahi tha na us samay..
33No elongation is Lθ/2 only... for the combined springs...(have used combination..)
If you consider each spring separately then elongationin each spring would be Lθ/4 but then u have to multiply (1/2)(k)(Lθ/4)2 by 2 (for both the springs...)
Note: i replied to the q but it had been deleted... above me... :P
33Din't used Lθ/4 bcause many have habbit for taking series parallel in springs also... so wanted to solve familiar to them as this had some other concept to learn.... something must sound them familiar.. ;)
33[11] u deleted ur post...
i am talking wid whom....
i'll sound crazy.. [3]
62Hint: Change of length of spring compensates the reduced length of the inextensible rope!
62I think there is a better / more crucial thing about this problem...
The constraint equation!
I am almost certain that most ppl will make a mistake in the constraint equation by taking
extension of the two springs to be x and 2x!
Think over it.. it is not x and 2x!
And this will not be found using the conventional methods of constraint equations but with a little presence of mind!
62It is confusing on the first look... but trust me you will enjoy it when u realise.
It is a sort of one of its kind problem!
But it is a must solve :)
I wont give more hnt than saying that the constraint equatino is not
governed by x1=2x2
1well......i m having a feel dat... both the extensions will be same i.e. x
'coz...the springs are not attached to some rigid object so they can move n have the same extensions (also spring constants of both springs are same...)
62The most important thing that remains is
Lθ = 4x
Where x is the extension in the spring!
If you did this correctly, everything else should be a matter of being careful :)