qwerty : justify P being thre ICR.
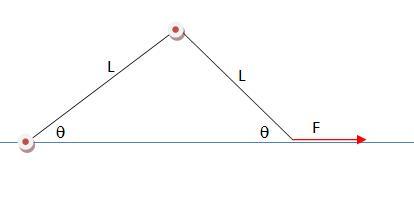
The setup shown consists of two identical rods (mass m) hinged together at the ends.
This setup is held in the position shown.
Now we start applying a constant force F to the free end as shown
Find the initial angular acceleration of the rods.
-
UP 0 DOWN 0 5 39

39 Answers
by the way i was restlessly waiting for some responses by some experts in this thread...
still waiting though...
Ok try doing it by energy method..
Write total enery = cons and differentiate ..
i wil giv it a try though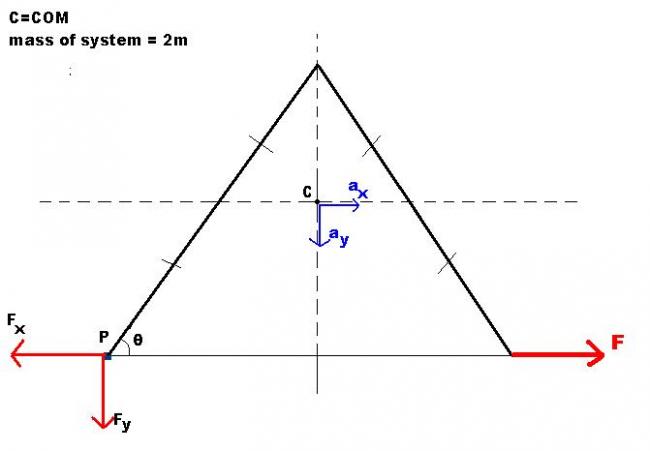
\tau _{c}=I_{c}\alpha
(F-F_{x})\frac{l}{2}sin\theta +F_{y}lcos\theta =I_{c}\alpha............................(1)
F-F_{x}=2ma_{x}
2mg+F_{y}=2ma_{y}
a_{c}=a_{x}(\hat{i})-a_{y}(j)
now Point P is ICR .
Hence COM performs pure rotation abt pt P.
thus ,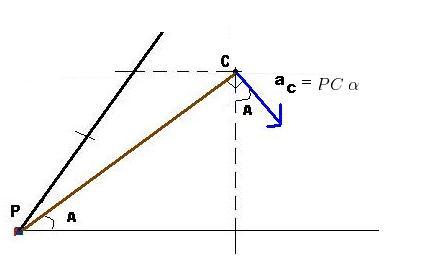
i.e,\vec{a_{c}}=PCsinA\alpha (\hat{i})-PCcosA(\hat{j})
i.e,\vec{a_{c}}=\frac{l}{2}sin\theta \alpha (\hat{i})-lcos\theta \alpha (\hat{j})
hence
F-F_{x}=2ma_{x}=2m\frac{l}{2}sin\theta \alpha =ml\alpha sin\theta
2mg+F_{y}=2ma_{y}=2ml\alpha cos\theta
putting the values of F-Fx and Fy in torque eqn
(ml\alpha sin\theta )\frac{l}{2}sin\theta +(2ml\alpha cos\theta -2mg)lcos\theta =I_{c}\alpha
\frac{ml^{2}sin^{2}\theta \alpha }{2} +2ml^{2}cos^{2}\theta \alpha -I_{c}\alpha =2mglcos\theta
\alpha = \frac{2mglcos\theta }{\frac{ml^{2}sin^{2}\theta }{2} +2ml^{2}cos^{2}\theta -I_{c}}
I_{c}=\frac{2ml^{2}}{12}+\frac{2ml^{2}cos^{2}\theta }{4}
\alpha = \frac{2mglcos\theta }{\frac{ml^{2}sin^{2}\theta }{2} +2ml^{2}cos^{2}\theta -(\frac{2ml^{2}}{12}+\frac{2ml^{2}cos^{2}\theta }{4}) }
\alpha = \frac{6gcos\theta }{l(3cos^{2}\theta +1) }
it can be done even widout ICR
system rotates abt com with alpha
so ap = ac/p+ap=CPsinA(i) - CPcosA(j) + ax(i) -ay(j) = 0
hence ax=CPsinA , ay=CPcosA
correction in last post ,
ap = ac/p+ap=CPsinA(-i) + CPcosA(j) + ax(i) -ay(j) = 0
@eureka : that was a reply to the general reader
to give them a complete picture lest they should commit the same mistake as virang1 did.
basically what i was pointing out was since there are both these forces present the choice of a point about which we can apply torque eqn is difficult to make.
.. specifically for your solution the torque due to gravity will definitely be zero.
it can be done widout ICR .........
the hinge at P is fixed , so its accn shud be zero ,see #29,30
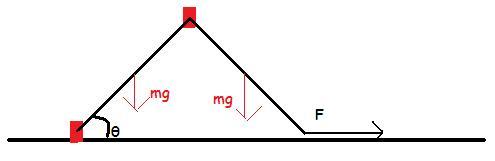
the above figure illustrates the initial condition...t=0
now at any arbit time t let the angle be β
now look at time t the angular velocity of both the rods will be the same by symmetry and the rod towards right will have traslational motion apart from its rotational motion...
thus we get,
mgl(sinθ-sinβ)+2Fl(cosβ-cosθ)=12Iω2+12Iω2+12mv2
v=l.ω (i.e. vel of top most point of leftward rod)
gives,
mgl(sinθ-sinβ)+2Fl(cosβ-cosθ)=Iω2+12ml2ω2=13ml2ω2+12ml2ω2=56ml2ω2
i.e. mgl(sinθ-sinβ)+2Fl(cosβ-cosθ)=56ml2ω2
differentiating we get,
56ml2.2ωα=-(mglcosβ)ω-(2Flsinβ)ω
gives α = - 6(mgcosβ+2Fsinβ)5ml
i hope that is the answer!!!
subho has done it correct
energy method se hi karna chahiye like subho
btw subho nice solution yaar
never thought abt doing it the energy way
btw subho pls point out da mistake in my solution
right....
the first rod is ok but to the right rod the COM has Accn as well as angular accn and these two things are related as a=Lα
also another forward accn of the right rod a'=α(L/2)
i think u missed on this!!!
and also you did not notice that |α| should be same for both :( even though i mentioned it in post #13 itself
i sense that this sum will involve the basic definition of angular velocity .... dθ /dt !
....or is it ....?
First of all notice that the magnitude of α will be the same for both...
I am not too keen to give any further hint because that hint will be the solution itself.
maybe after someone has atleast tried
First resolve the force F one perpendicular to the rod and another along the rod.
Therefore Fp = Fsinθ
Fa=Fcosθ
Now Fa will produce x acceleration to the rod in its direction. Therefore
Fa = 2mx
x=Fa/2m
Now this mx will be the force that will provide the torque to the left hand side rod.
Therefore now angular acceleration
For the left one
mxl = ml2/3*α
α=3x/l=3Fa/2ml=3Fcosθ/2ml
For the right one
FpL = mL2/3*α
α=3Fp/mL
α = 3Fsinθ/ml
no.......
you seem to have left out all the forces except F.....
! ? [11]
how do you justify that
@virang1 : did not want to discourage the only person who tried....
but honestly u are not even close.