This is a marathon for Physics ie., IT continues for long. A user posts problem, the next posts the solution and ANOTHER problem to be solved by the subsequent one and this Continues.
Problem 1
A uniform rod of length 
, mass 
is hinged at one of its ends and is free to rotate in vertical plane. It is released from rest in horizontal position. At 
, when the rod becomes vertical, it is broken at midpoint and as a result the lower part now moves freely.
Find the the distance moved by the center of separated lower part from hinge until it again becomes vertical for the first time during the subsequent motion. HINTS: Note that the rod which is separated will still have some angular velocity.
71Problem 2
A wire of mass \mathcal{M} , Length \mathcal{L} and tension \mathcal{T} is clamped at both ends and is set into vibration such that it vibrates in its Fundamental Mode. At the midpoint of the wire, the Amplitude is \mathcal{A}_\bf{0}.
Find the maximum Kinetic Energy \left(\mathcal{E}_\bf{K}\right) of the wire?
Previous Problem : I agree with Aditya!
71Problem 3
A heavy disk with radius R is rolling down hanging on two non-stretched strings wound around the disk. The free ends of the strings are attached to the disk. The strings are always tense during the motion. At some instant, the angular velocity of the disk is ω , and the angle between the strings is α (fig.3.0).
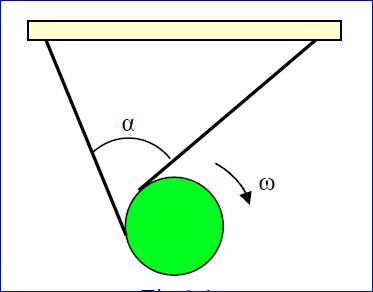
Fig 3.0
Find the velocity of the disk at this moment.
Hint: There is not very much Computation involved in here. It's conceptually strong question.
71Yes Swaraj logic is correct. In a Standing wave, different particles have different maximum amplitude, but since ω is same for all the particle sof the string, the KE max of the different particles will be different.
A general expression for a standing wave can be written as y = 2a sin (kx) cos (wt) .. (Since we have a node at x=0), (a is the amplitude of the original wave)
Where A = 2a sin(kx) , Now given that at x = L/2 , A = A0 , You'll get after putting value of k that A = A0 sin (kx) i.e., 2a = A0.
Hence, Vmax = A.ω = ω . A0 sin (kx)
Hence, KEmax = 12 (dm) (vmax)2
Where (dm) = Ï (dx)
Integrate this to get answer as EK = ω2ÏA022 [ L - sin (KL)K ].
There might be some computational mistake.
1@swaraj: see what u get if u integrate the fnctn..u shud get the same answer only....
@vivek:can u pls verify?
21For a string fixed at both ends.
We know v=Awsin(wt)
Now, the max velocity of a particle at diff. pts in the string is diff. due to diff. max amplitudes.
Hence we have to integrate,for each dx length of the string along with their diff. max. velocities.
If you are not convinced with the fact that diff. particles have diff. max velocities,and think that when particles cross their mean pt. they all have same velocity then consider the following explanation:
First think of normal wave propagation.As the energy is getting transferred each particle acquires max. energy as the wave propagates and at some time or the other.
But when the wave is confined the energy distribution is not uniform, but constant depending on the mode of vibration and position.eg in 1st overtone the max. energy is confined in two positions which are at a distance of L/4 from both ends.
262@debosmit - the question asks the maximum value of KE , so there is no need to take rms value
@swaraj - i didnt get your post.
21Aditya method is fine but he missed something.
KE=1/2*Mvmax2=1/2*M(Aω)2[Here A is not A0 but varies as sine funct. hence we have to integrate]
1i guess the answer should be Aditya`s answer divided by 2 that is
pi2A02T/4L
we should take rms value of the max amplitude
71Aditya, It is wrong. If I tell something, It'll be the solution itself. Hint: This KE is not the KE of wire.
262KE max = 1/2*M*(vmax)2 = 1/2*M*A02 *w2 (since vmax =A0w)
now w = 2pi*f
v=f*(2L) (since wavelength = 2L)
v=√TLM
substituting all these values ,
KE = pi2 A02 T2L
262i am getting a really ridiculous answer .
btw do we need to find only the horizontal distance or total distance ?
71Even I got similar to what you get.. Can't call up exactly. Will work out in a very detailed manner tomorrow. The swaraj's answer looks terrible.
21I never said momentum will change.
Momentum(angular) will not change.The only force acting here is the contact force which passes through the pt. of rotation and hence exerts 0 torque.
Aditya- one question?In your approach around which pt. does the detached body rotate.
262let w be the angular velocity just before snapping.
after detachment , Vcm(of lower part) = w*3L/4 (as CM of lower part is at a dist 3l/4)
w = dQdt (Q=angular displacement)
t =Q/w = pi /w (since after rotating by an angle pi , the part becomes vertical again)
distance moved by lower part = Vcm* t = pi * 3L4
21I think The velocity of the other part of the rod will also change.
262even i think it will not change.
since the other part of the rod will also have the same angular velocity .
71Swaraj, I don't think w for the broken rod should change?
21Apply conservation of linear and angular momentum.
Initial vel. in horizontal direction=final velocity in that direction=3/4*ωL [i.e. of C.M. and will be same as mass of detached part does not change]
Now for conservation of angular momentum:
Initially it was revolving around hinge.After detachment it will revolve around C.M.
ω1I1=ω2I2
Solving ω2=28ω
Horizontal distance covered=v*t=(3/4*ωL)(π/28ω)=3πL/112(ans)