3SKY ITS STANDARD... WHEN SPRING HAS MAX. EXTENSION ... IT BEHAVES IN SUCH A WAY THAT BOTH HAVE A COMMON VELOCITY .. THINK PRACTICALLY ULL UNDERSTAND...
20 Answers
3
3yeah..i too did the same thing...common velocity at max extension...
lekin phir expression bahut complicated aa rahaa thaa...
3NO I ALWAYS TYPE LIKE THIS.......[3]..
IF THERES SUM EXTENSION ILL ADD 1/2KY^2 ON THE LHS OF MAH SECOND EQXN... DATS ALL.......
1and yeah,,, i also didn ask wat is the necessity of such an assumption... i wanted to ask... y shud u at all make one such... wen nothing like dat is mentioned//
1wellif in case, there is some initial extension... WHAT ARE U GOING TO DO??
(btw, y are u talking in capitals?? shouting or wat?? ... u dont have smal letters in your PC :P :P :P)
3CUZ THEN MY ""COME"" EQXN. WILL CHANGE ........ ITS USUALLY GIVEN IN QUESTION ALL DAT STUFF.... HES GIVEN HALF QUESTION..........THOSE TRIVIAL THINGZ BECME QUITE IMPT.
1areyyyyyyyy maine yeh nahi poochhi....
main was asking... y u assumed initial xtension is 0??
3IF U STILL DONT UNDERSTAND ... HERES A GUD WAY OF TAKIN IT ..........
IN A SPRING WHEN ITS AT MAX EXTENSION..........ITS LENGTH REM. SAME ............
SO APPLY CONSTRAINTS ...... ULL GET THIER VELOCITIES TO BE SAME....[1]
33[13]
yaar atleast give m, 2m ... u, 3u something like this for easier calculation ....
106sky tumne wahaan kya kiya hai??? mere dimaag ke upar se ud gaya...
3AT MAX EXTENSION BOTH HAVE COMMON VEL. SAY @ m/s .....
cons. momentum ...
MV - mu = (M+m)@ .(1)
COME
1/2MV2 + 1/2mU2 = 1/2(M+m)@2 + 1/2kX2 .......
find x ........
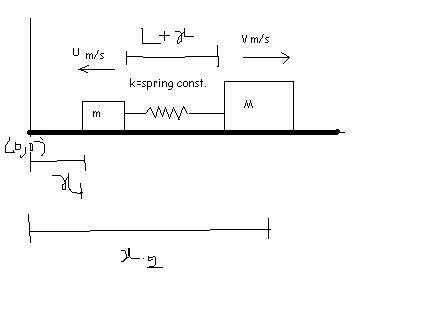
assumin initially extension of spring is 0!!!!![1]
1x2 = x1 + x + L
=> v = -u + dx/dt
=> a2 + a1 = d2x/dt2
=> -kx/M - kx/m = d2x/dt2
=> ω2 = k(1/m +1/M) --------- (1)
so, x= A sin(wt + φ) ---------------------(2)
dx/dt = Aω cos(wt + φ)
at t=0, dx/dt= v-u = Aωcosφ -----------------(3)
at t=0, acc=0 => Aω2sin(φ)=0 => φ=0
from (3) , v-u = Aω => A= v-u/ω
wat is the ans??
13ok... take...... M=2m..... V=3U....as u wish....[4]