http://targetiit.com/iit-jee-forum/posts/constraint-equation-471.html
This thread doesn't explains so much (especially the energy method). I urge nishant sir or anyone who has that much patience, to explain this term/concept more clearly to us.
How to find the wedge constraint using the method of "net Work done by internal forces (in a system) is zero. "
http://targetiit.com/iit-jee-forum/posts/constraint-equation-471.html
For example, in the below figure..suppose the wedge is accelerating with a m/s2 . How to find the acc of block w.r.t ground and w.r.t wedge.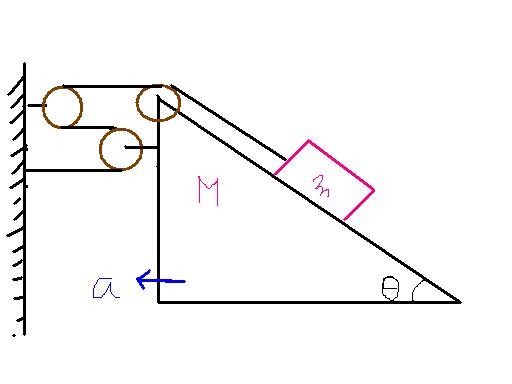
http://targetiit.com/iit-jee-forum/posts/constraint-equation-471.html
This thread doesn't explains so much (especially the energy method). I urge nishant sir or anyone who has that much patience, to explain this term/concept more clearly to us.
Is the answer with an acceleration 3a along the downward direction parallel to the inclined plane??
the simple sol is easy enough
the acc of m is twice of that of M
and the tension on the block is 3t
therefore mgsin@-t=2ma
and 3t=Ma
net work done by internal forces on a system is zero...because positive work and negative work cancel each other...from this we can conclude Tension(along the direction of acc) is inversely proportional to acceleration..
i got acc of the block along the incline is a(3- cos∂ )
yup the acc of block along the incline is a (3 - cos theta)
but how ??
(1)in ground frame, as string doesnt slack , hence work done by string = 0
T(a)+T(a)+T(a)+T(a)(-cosθ)=T.am = (T)(am,along incline)
hence am,along incline = 3a - acosθ
if u dont get this,
(2) in wedge's frame ,as string doesnt slack in dis frame also , hence work done by string = 0
hence Σ T. a = 0
now in wedge's frame , left wall is having accn a in +ve direction
T(a)+T(a)+T(a) =Tam/M
so am/M = 3a ..along incline and downwards
or am/M = 3acosθ (i) - 3asinθ (j)
aM = -a(i)
am = am/M+ aM = (3acosθ - a) (i) - 3asinθ (j)
now consider a unit vector along the incline , \hat{n}= -cos\theta (i)+sin\theta (j)
now \vec{a_{m}}.\hat{n}= component \; \; of \;\;a_{m}\;\;along\; \; incline
= -(3acosθ-a)(cosθ) - 3asinθ(sinθ) = acosθ - 3a
or 3a-acosθ down the incline