1ans none of these ???
A disc of mass 2M lying in vertical plane is free to rotate about a fixed horizontal axis passing from its centre. A particle of mass M is tied to a string of length 2R and another end of the string is attached to the disc as shown in figure. If particle is released from shown position, then the angular speed of the disc as string becomes taut will be
(a)√2g/R
(b)√g/2R
(c)√g/4R
(d) none of these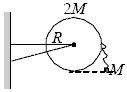
-
UP 0 DOWN 0 0 15
15 Answers
1arey..
conserve energy about the point owhere the thread is attached...
62First find the velocity of the mass in the downward diirection
then find the angular momentum.. MVr about the center of the cylliner
then conserve angular momentum about the center.
1no i din mean conserve energy ....
i meant work-energy theorem...
1/2Iw2 = mgR
am i wrong ??!#@$
106the ans. is given (b)
@nishant bhaiyya: how can we conserve angular momentum? there will be a net torque at the point on rim when string becomes taut. So, torque ≠0
62what I are u using..
I wud rather give this solution...
1/2mv2=mgR (It will gain a height of R not 2R)
so v=√2gR
now we conserve angular momentum about the center of the cylinder..
So MvR=M√2gRR=(2m)R2/2. ω+ M(ωR)R
√2gR=R. ω+ (ωR)
So ω=√g/2R
62yes u are right.. my mindgame failed... :)
writing it down got me a more correct answer :)
62about the center there is no external torque because we are using the center as the hinge..
The torque due to gravity acts for avery little time.
It is the same reason why we conserve linear momentum even when there is mg acting as an enternal force.