D
Two identical blocks are released from the top of two fixed wedges of same height(h) and same base length (l). The speeds of the blocks when they reach the ground are related by( k is the coefficient of friction in both)
(A) vA=vB
(B) vA>vB
(C) vA<vB
(D) Cannot be determined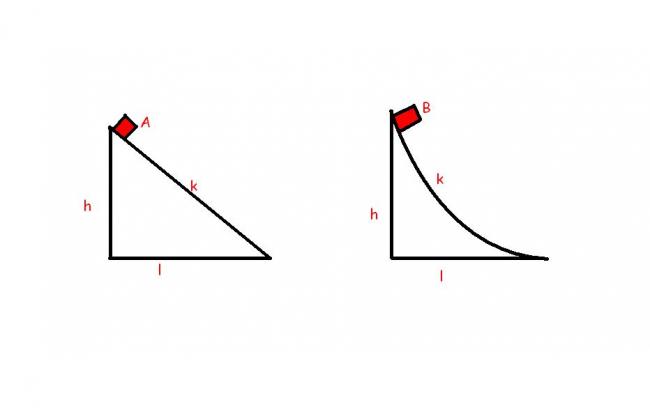
-
UP 0 DOWN 0 1 13

13 Answers
joh bhi answer karo solution do :) mera doubt hai aur answer nahiin mila.. Irodov karte wakt yes doubt aaya tha
ok then we have to consider the non conservative nature of the frictional force.due to this force the the internal energy of the block changes so we cant determine the ratio of the gravitational energy that gets converted into KE of the block.for more ideas read NCERT
A)
See ideally(w/o friction)
mgh = mv2/2
But there is friction
mgh = mv2/2 + Work done by friction
Now Work done byu friction
=k N*dr
N = Normal force
In 1 the normal force is more than 2
While dr is more in 2 than 1
Therefore Work done by friciton will be equal Therefore velocity is will be equal
but virang how do u know that N*dr in both cases is same? even if N in 1 is more than in 2 and dr is more in 2 but how do u know that they will be EQUAL ?
luk the radius of curvature of a is infinite...and dat of b is say R(finite) at some instant...
by work energy theoram,
Wg - Wf =1/2mV2
for b, at any given instant when the velocity of the block is 'v', at an inclination ∂, we have
N-mgcos∂=mv2/R
or we have N=mv2/R+mgcos∂
F= k(mv2/R+mgcos∂)
work by friction=-\int K(mv^{2}/R +mgcos\delta )ds
=-{\int K(mv^{2}/R)ds +K(mg)\int (cos\delta )ds}
=-{\int K(mv^{2}/R)ds} - Kmgl
as integration of cos∂ds=l
now going to the situation of a,
we have work done by friction is simply -Kmgl...
we see that extra negetive work is done in the case b, so
by work energy theoram,
kinetic energy of the block at b. is lesser that that of a
hence
B)
cheers!!!
What if:
2nd CAse
at any time, let the angle of inclination with horizontal be θ.
Then let the speed of the block be v
Let it move a distance dr and let corresponding increase in velocity be dv
So, dK = dW (WE theorem)
\frac{m(v+dv)^2}{2}-\frac{mv^2}{2}=mgsin\theta *dr - kmgcos\theta *dr
OR mvdv = mg(drsin\theta )-kmg(drcos\theta )
vdv = gdh -kgdl
integrating
v^2/2 = g(h-kl)
In first case:
\frac{mv^2}{2} = mgh - kmgcos\theta *\sqrt{l^2+h^2}
\frac{v^2}{2} = gh - kg\frac{l}{\sqrt{l^2+h^2}}*\sqrt{l^2+h^2}
\frac{v^2}{2} = g(h - kl)
which is same as in first case
nice work, but the place where i find a flaw, is
the frictional force is not Kmgcos@ but is KN
here N is not mgcos@ but N is given by
N-mgcos@ = mv2/R
or N=mv2/R +mgcos@
it is that "mv2/R" that makes the difference between the 2...
cheers!!!
if u consider a small displacement then u can regard it as a straight line hence mv2/R wont come into the picture. then why shud we consider the term mv2/R.
dude, ill try and contradict u...u say that the final velocity is path independent....if the same track was circular,u wud concider a flat part, and even here if u say that as its a flat part, it has infinite radius of curvature, u are wrong...in dat case why dont u analyse every circular motion in that way, i mean at every instant u concider a flat part, so der will be no centripetal force....
when u say a "flat part" its not the flat part that u exactly concider, its the "flat-path" that u concider at that instant...i mean for that instant the particle is moving at a tangent to the curve at that instant...
if u still arnt convinced, there is a theory in math for finding out the
"Radius of curvature of a given curve" at a point (x,y) on the curve...
so for any curve at any point, there exists a given radius of curvaature,
no matter how small a part of the curve u concider, at that instant, the particle under goes an instant centripetal force which is equal to
mV2/R where V is the velocity of the particle at that instant, R is the radius of curvature of the curve at the instant, which is purely geometrical,
if u still donot agree with me, ill suggest u better have some senior or a sir to come and have a look into this discussion...
cheers!!!