1yes tapan that is only what he has written jus think one more step ahead ....
32008+72008+2008
if divided by 28 what is the reaminder....
ans-1
please tell me how?????
-
UP 0 DOWN 0 1 29
29 Answers
11copy pasting my post #13 as it seems to have been lost
"is the answer written as -1 coz i am getting 28"
21@philip,
to ans wat u wer asking 4 proof in nishant sir's soln....
2008 = 2001 + 7;
= 29*69 + 7;
{i dunno how did sir get 20??? as 1988 aint div by 29 }
try out by wat i suggested
u'll get da ans.....
21oh shit........
made a fool of myself [9] [4]
yeah yeah........ FINALLY got ur point......
thnx dude.....
129K/3 is an integer from the third line of your very post tapan
21oh k k PHILIP now i got how r u wanting me 2 fashion my thinkin(hopefully)
BUT STILL A DBT REMAINS .... SORRY DUDE 4 HARASSIN U SO MUCH.........
3^29 - 3 = 29k;
3(3^28 - 1 ) = 29k ;
3^28 - 1 = 29K/3 ;
BUT HOW CAN U SAY THAT 29K/3 WILL BE AN INTEGER AS K MAY/MAY NOT B DIVISIBLE BY 3????????????????? [7]
BCOZ V GOTTA PROVE : 3^28 - 1 = 29P
WER P,K ARE INTEGRS
1ulta socho bhai agar 3^29 remainder 3 ka chor ta hai to 3 ^ 28 kitnne ka chorega?...
21THEN HOW DID SIR GET, 328≡1 (mod 29) USING ap≡a (mod p)
IF U HAV GOT IT CAN U PLZ POST IT HOW??? [7]
1no tapan we can't divide in congruences
i think there is something else to it
but think of what nishant bhaiyya did the other way round...
21@PHILIP PL REPLY TO THIS DBT OF MINNE....
@philip do u mean to say by dividing 3 on both sides u get 328≡1 (mod 29)
12≡4(mod 4)
divide by 4 on both sides....
3≡1(mod 4)
21SIR,
THIS WAS THE METHOD I WAS WORKING WITH..... EQUALLY LOOONG.....
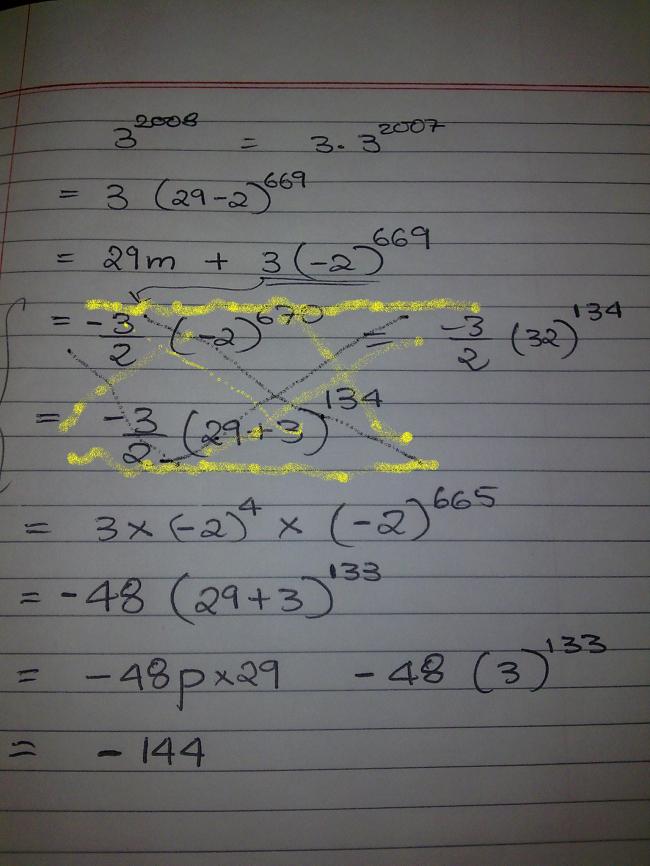
1no i bet my method is much more messy than urs
the idea of using fermat's theo like this never ocurred so you can make out how long my method must have been...
but please clarify your step of reducing 2008 to 20
21@philip do u mean to say by dividing 3 on both sides u get 328≡1 (mod 29)
but is dividing on both sides allowd in congruence modulo?? [7]
Nishant Sir has doe so has to be rite but i had a doubt,
c
12≡4(mod 4)
divide by 4 on both sides....
3≡1(mod 4)
[7] [7]
62yes philip they are the same..
do you have a simpler method.. I think the method by me is a bit messy for my own liking :(
21ap≡a (mod p)
then how does this follow?? [7]
328≡1 (mod 29) (fermat's theorem.. not in syllabus)
shud it not b sumthing like : 329 ≡ 3(mod 29) ????
1bhaiyya i can't get that step
3^2008-1988+7^2008-1988+2008-1988 [7][7]
62no this is not in IIT JEE syllabus.
it is a theorem which says that
ap≡a (mod p)
But this is not in IIT JEE syllaubs
What is expected from you in an IIT JEE exam is that you are able to solve the problems that need binomial theorem.
11328≡1 (mod 29)
please explain this in a bit more detailed fashion
and are such type of expected to appear in jee or aieee
6232008+72008+2008
if divided by 29 what is the reaminder....
328≡1 (mod 29) (fermat's theorem.. not in syllabus)
thus 31988≡1 (mod 29)
and similarly
728≡1 (mod 29)
71988≡1 (mod 29)
Now you can take it from here..
32008-1988+72008-1988+2008-1988 (mistake pointed by tapan )
if divided by 29 what is the reaminder....
=320+720+2008
if divided by 29 what is the reaminder....
21YEAH!!!!!!!!
me 2 gettin ans 10 after dividing by 29 [7]
but unfortunately the ans raeds 1 [2]
1132008 = 3*(32007) = 3*(27669) = 3*((28-1)669) = 28m - 3
So 32008 / 28 gives remainder = 25
72007 = (8-1)2007 = 4n - 1
So 72008 / 28 gives remainder = 3
So 32008 + 72008 / 28 gives no remainder
502 = (497 + 5) = 7k + 5
So 2008 / 28 gives remainder = 5
Hence [ 32008 + 72008 + 2008 ] / 28 gives remainder = 5
I don't understand how the ans given is 1 [7][7][7][7]
Somebody correct me if I'm wrong!!