m not very sure bout the question.
Q1)In a year proove that the 13th day of some month are friday.
Q2)For the given gragh area of OAP=area of OBP and AP and PB is parallel to y and x axis respectively.find f(x)....(O=(0,0))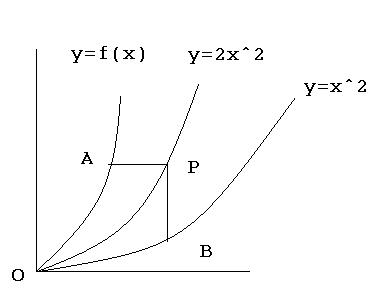
Q3)let n be postive integer then proove that the sum of every odd 8n+4 consecutive integer is not a perfect square.
-
UP 0 DOWN 0 0 4

4 Answers
1) let the 13th of jan be day X
then 13th of feb will be X+2;
mar- X+2
apr- X+4
may- X+5
june- X+7=> X
july- X+1
aug- X+3
sep- X+5
oct- X+6
nov- X+8=> X+1
dec- X+2
hence atleast one of the 13ths will be a friday
the above soln was for a normal year.
for a leap year change for mar as X+3 and proceed as above.
Q3)let n be postive integer then proove that the sum of every consecutive integer 8n+4 times is not a perfect square.
i did not get the question!
Is it the sum of 8n+4 consecutive integers?
If you calculate, for each month in a non-leap year, the number of days preceding it in the year mod 7, you get
J...0
F..3
M..3
A..6
M..1
J...4
J...6
A..2
S..5
O..0
N..3
D..5
If you do the same for a leap year, you get
J...0
F..3
M..4
A..0
M..2
J...5
J...0
A..3
S..6
O..1
N..4
D..6
In either case, every number, from 0 through 6, occurs at least once every year. That means that, regardless of what day the year starts on, every day of the week will be represented as starting off a month at least once that year. The same is true for other days of the month, such as the 13th. The 13th of the month will fall on each of the 7 days of the week at least once every year.
We can see more from these tables. It is possible to have just one Friday the 13th, or as many as three in one year.
If a month is going to have a Friday the 13th, it has to start on a Sunday. This will happen three times in a leap year if the year starts on a Sunday. The three months will be January, April, and July, where the three 0's are in the leap year chart.
For non-leap years, we get Fridays on the 13th in February, March, and November whenever the year starts on a Thursday. These are where the 3's are in the first chart.
The numbers that appear just once in each chart, the 1, 2, and 4 in the first chart and the 1, 2, and 5 in the second, mark months that can have a lone Friday the 13th.