24Thanx for confirmation....
btw it will be a2 in denomiantor and not a
this particle mass m moves in a box forth and back with speed v.Considering matter wave associated with particle and knowing that due to back and forth motion standing waves will be produced in box,find
a)min.energy to excite particle from ground state to higher state
b)Quantum number of particle as in Fig2
-
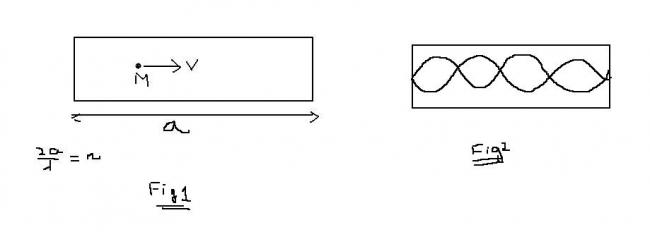
UP 0 DOWN 0 0 2
2 Answers
66The wavelength associated with the matter wave is
\lambda =\dfrac{h}{p}
where p is the momentum
The allowed values of the momentum is determined by the boundary condition
a=n\lambda/2\quad\Rightarrow \ n\lambda = 2a
i.e. the allowed momenta are given by
p=\dfrac{nh}{2a}
Hence, the allowed energy states are
E_n=\dfrac{p^2}{2M}=\dfrac{n^2h^2}{8a^2M}\qquad n=1,2,\ldots
So the transition from the ground state to the next state requires an energy difference
\Delta E_{1\to 2}=\dfrac{3h^2}{8a^2M}
P.S. edited to make that a to a2
24