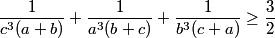341Rahul, check your steps from (2) onwards. The logic ain't right.
9 Answers
1ok let us consider a<b<c
we have 1/a3(c+b)>1/b3(a+c) and also 1/a3(c+b)>1/c3(a+b) .....(after addin we get)
3/a3(c+b)> 1/a3(c+b)+1/b3(a+c) +1/c3(a+b)≥3/2
now to prove dat 3/a3(c+b)>3/2 would be sufficient
to maximize 3/a3(c+b) we gotta minimize denominator
c>a b>a.....(after addin we get)......(1)
c+b>2a
this implies dat a3(c+b)> a3(2a)........(2)
now a+b+c>3...(from A.M G.M ineuality n itz given dat abc=1)
a+b+c>3a..(from (1))>3
this implies a>1
terefore eq(2) changes to a3(c+b)> a3(2a)>2
hence prooved that
3/a3(c+b)>3/2
since 3/a3(c+b),the max value of initial expression is >3/2
.......the expression is also >3/2.......:)
66Let
a=\dfrac{1}{x},\quad b=\dfrac{1}{y},\quad c=\dfrac{1}{z}
Then we have xyz = 1.
The given inequality becomes the same as
\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\ge \dfrac{3}{2}
Cauchy Schwarz imply that
[(y+z)+(z+x)+(x+y)]\left(\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\right)\ge (x+y+z)^2
That is
\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\ge \dfrac{x+y+z}{2}
But then by AM-GM
\dfrac{x+y+z}{3}\geq \sqrt[3]{xyz}=1
Hence,
\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\geq \dfrac{x+y+z}{2}\geq \dfrac{3}{2}
341
1It's quite simple SHORTCUT METHOD
Since abc=1
Therefore, let us take a = 1/2 ,b=1, c=2
Putting these values in the inequalities, we get
[1 / (2) 3 ((3/2) ]+[ 1 / (1/2) 3 (3)] + [1 / (1)3 (3/2)]
which is greater than 3/2.
341This is a fairly well know problem [IMO 1995].
But here's a solution which uses just AM-GM and I have not encountered this method so far in my readings.
From AM-GM
\frac{1}{a^3(b+c)} + \frac{a(b+c)}{4} \ge \frac{1}{a}
Since abc = 1, we can rewrite this and the other two similar inequalities as:
\frac{1}{b^3(c+a)} + \frac{1}{4} \left[\frac{1}{c} + \frac{1}{a} \right] \ge \frac{1}{b}
\frac{1}{a^3(b+c)} + \frac{1}{4} \left[\frac{1}{b} + \frac{1}{c} \right] \ge \frac{1}{a} and
\frac{1}{c^3(a+b)} + \frac{1}{4} \left[\frac{1}{a} + \frac{1}{b} \right] \ge \frac{1}{c}
Adding the three and grouping you get \sum_{cyc} \frac{1}{a^3(b+c)} \ge \frac{1}{2} \left[\frac{1}{a} + \frac{1}{b} + \frac{1}{c}\right]
But from AM-GM we have \frac{1}{a} + \frac{1}{b} + \frac{1}{c}\right \ge \frac{3}{\sqrt [3] {abc}} = 3
and hence the original inequality follows
341See http://www.mathlinks.ro/viewtopic.php?p=365178#365178 for more discussion
1ok thanks prophet sir i got my mastake.
your and kaymant sir's solutions are great
i got this question from http://www.artofproblemsolving.com/Forum/weblog_entry.php?t=264227
could you please how to solve this using titu's lemma
341But kaymant sir has already done that Σx2/(y+z) ≥ (x+y+z)2/2(x+y+z) is by Titu's lemma isnt it?