LOL!u guys have pledged not to leave any inequality unsolved???[3][3]
if got some time plz reply to progressions-4
3 .
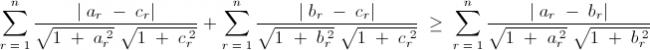
" a r , b r and c r" are three sequences of real numbers .
We will prove the inequality |a-c|(√1+a2)(√1+c2)+ |b-c|√(1+b2)√(1+c2)≥|a-b|√(1+a2)√(1+b2) is true.(a,b,c are real)
That doesn't remind of any direct inequality. Tried simplification ,it became more complex. the inequality is not symmetric , not homogenous ,neither direct modulus inequality. Tried using trigonometric replacements. It's quite natural to take a = tanA , b = tanB , c= tanC (all the angles A,B,C lies between -pi/2 and pi/2)
The inequality boils down to |sin(A-C)| + |sin(C-B)|≥|sin(A-B)|=| sin{(A-C) + (C-B)}| =|sin(A-C)cos(C-B) + sin(C-B)cos(A-C)|
we have |sin(A-C)|+ |sin(C-B)| ≥|sin(A-c)||cos(C-B)| + |sin(C-B)||cos(A-C)|
(Note that |cosx| lies between 0 to 1)
≥|sin(A-C)cos(C-B) + sin(C-B)cos(A-C)| (by modulus inequality)
LOL!u guys have pledged not to leave any inequality unsolved???[3][3]
if got some time plz reply to progressions-4
though Ricky did nt say anything,the solution is correct according to me..