341perhaps he had an equilateral triangle and pigeonhole principle in mind
All points of the plane are colored red, blue or green. Prove that we can find two points a distance 1 apart with the same color.
-
UP 0 DOWN 0 2 19
19 Answers
341
1
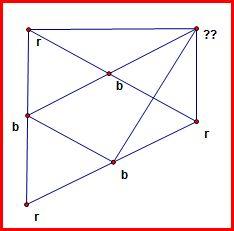
Existence of the equilateral triangle of side=2 (the r-r-r triangle) is established.
Now to avoid the condition, The midpoints are blue.
Then contradiction occurs for coloring the shown point.
1Yeah. But this type of problems always admit a solution using geometrical figures which is easier to find.
62ith power, cant we prove because we have proved already that the equilateral triangle exists, so by scaling the plane suitably (coordinate axes) we can get a right angled triangle of some size
and as soon as we get a right angled triangle of some dimenstion by scaling the axes again we can get a right angled triangle of the dimension that you want?
39ya. we can do that also.
but i tried to make things as simple as possible
1YEP.
A harder one:
Show that there exists a monochromatic triangle of side 1,√3,2 . [in bicoloring the plane].
39ith power --
pick a distance d
pick a point; say it's red
draw a circle of radius d about it
if there is a red point on it, we're done
otherwise, every point on the circle is blue
pick a point on the circle and draw a circle of radius d about it
the circles intersect at a point which must be both red and blue; contradiction
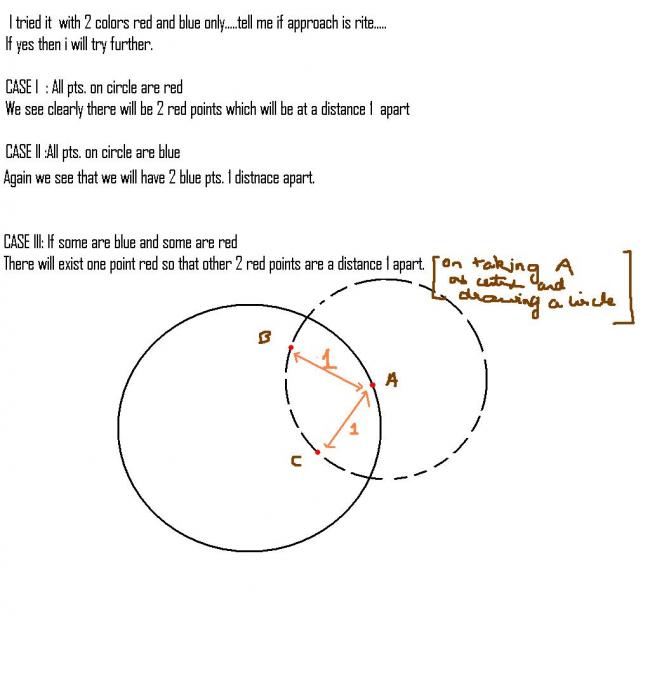
1proceed by assuming the contary.
consider two fused equilateral triangle of side 1 giving a rhombus. let it be ABCD.
Now if A is red, B is green(or blue) and C is blue(or green). So D is red.
Consider circle of radius √3 around A.
All points on the circle are locus of D. So the circle is red. then there is a unit lenghted chord.
Follow up question:
If two colours are used, prove that we can get two oints of same colour any d distance apart.
[its pretty easy but the method is ingenious]
