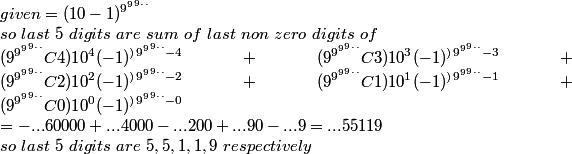final 5 digits

Sorry Rahul, what you have done is not correct. Not all terms of the sum
- ....60000 + ....5000 - ....500 + ....00 - ...1
are correct.

oh sorry. here are the correct ones
...00000 + ...5000 - ...500 + ...10 - ...1 = ...04409
is this correct?

well even that is not correct. think a bit more because you are going in the right direction..

a = 9⁹ = (10-1)⁹ = ⁹C₀10⁹ +....+ ⁹C₈10¹(-1)⁸ - 1

last two digits are 90-1 = 89

so, a = 100p + 89

b = 9⁹⁹ = (10-1)^a

last 3 digits are given by -^aC₂10² + ^aC₁10 - ^aC₀

≡ - 100(a-2)(a-1)2 + 10a - 1

≡ - 50(100p+87)(100p+88) + 10(100p+89) - 1

≡ - 600 + 890 - 1 ≡ 289

so b = 1000q+289

c = 9⁹⁹⁹

similarly proceeding last 4 digits of c are 5289

d = 9⁹⁹⁹⁹

last 5 digits are 45289

as we increase nines the ending digits remain same as can be observed when we move from a to d

so last 5 digits of 9^999.... (1001 nines) are 45289