391)
If p,q,r denote the three distances from the vertices and `a` is the side of the equilateral triangle
then we have 3(p^4+q^4+r^4+a^4)=(p^2+q^2+r^2+a^2)^2 (try proving yourself)
1)in an equilateral triangle of side a, the distance of a point P from its vertices is given 3.4 and 5 respectively.FIND THE VALUE OF THE SIDE a.
2)On similar ground try to to find the side of a square ABCD such that the distance of apoint p from its vertices A,B,C is 3,4,5 respectively.
3)prove this question by pure geometry.
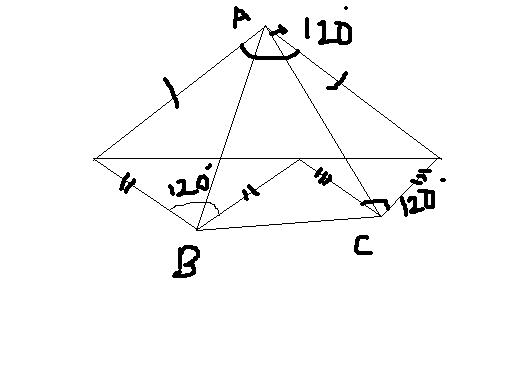
PROVE THAT ΔABC is equilateral.
-
UP 0 DOWN 0 0 3
3 Answers
39
11Exactly you cannot solve this question by conventional methods and zorro idont get the ans by your identity.
THIS POSTS HEADING IS PURE GEOMETRY AND SO USE ONLY PURE GEOMETRY.