21
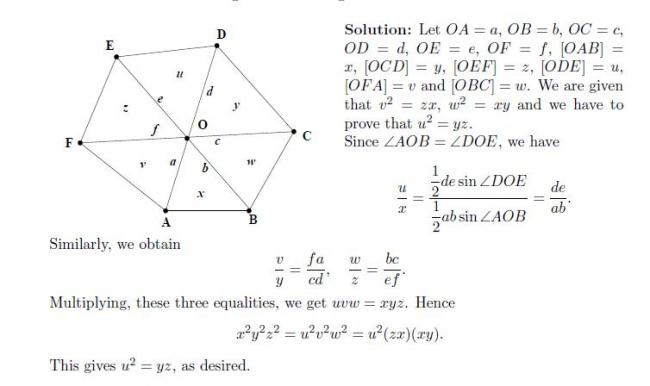
Let ABCDEF be a convex hexagon in which the diagonals AD, BE, CF are concurrent at O. Suppose the area of traingle OAF is the geometric mean of those of OAB and OEF; and the area of triangle OBC is the geometric mean of those of OAB and OCD.
Prove that the area of triangle OED is the geometric mean of those of OCD and OEF.
-
UP 0 DOWN 0 0 3
3 Answers
21Not all convex hexagons has concurrent diagonals
we will construct the required hexagon using three concurrent lines.
we will use
Area = 1/2 ab sin ∂
we would have got 16 marks in 5 minutes in RMO 2010,Dec 05 ;(
36question from RMO 2010......
simply use, area of triangle ABC with angle O between AB and AC is given by 1/2 x AB x AC x sin O