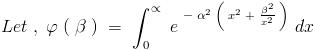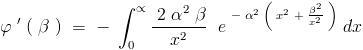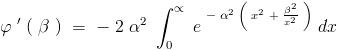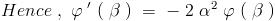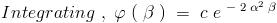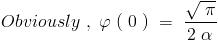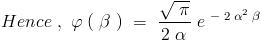1R u sure u r getting the recurrence u have written?
This problem(or anything comparable to this) will not be asked in IITJEE.
That's why i posted this in olympiad section.
Evaluate:
\int_{0}^{\infty}{e^{-\alpha^2\left(x^2+\frac{\beta^2}{x^2} \right)}}dx
You may use: \int_{0}^{\infty}{e^{-x^2}dx}=\frac{\sqrt{\pi}}{2}
-
UP 0 DOWN 0 0 8
8 Answers
11I don't think that it is correct either...
Here's my solution:
I(\alpha,\beta)=\int_{0}^{\infty}{e^{-\alpha^2\left(x^2+\frac{\beta^2}{x^2} \right)}dx} =\int_{0}^{\infty}{e^{-\alpha^2\left[\left(x-\frac{\beta}{x} \right)^2+2\beta \right]}dx} \\\\=e^{-2\beta\alpha^2}\int_{0}^{\infty}{e^{-\alpha^2\left(x-\frac{\beta}{x} \right)^2}dx}
Now differentiate both sides wrt \beta
So:
\frac{\partial I}{\partial \beta}=-{2\alpha^2\beta}\int_{0}^{\infty}{\frac{e^{-\alpha^2\left(x^2+\frac{\beta^2}{x^2} \right)}}{x^2}dx}
Now:
I-\frac{1}{2\alpha^2}\frac{\partial I}{\partial \beta}=e^{-2\alpha^2\beta}\int_{0}^{\infty}{\left(1+\frac{\beta}{x^2} \right)e^{-\alpha^2\left(x-\frac{\beta}{x} \right)^2}dx}
Take:
x-\frac{\beta}{x}=\frac{z}{\alpha} \\\\\Rightarrow \left( 1+\frac{\beta}{x^2} \right)dx=\frac{dz}{\alpha}
I-\frac{1}{2\alpha^2}\frac{\partial I}{\partial\beta}=\frac{e^{-2\alpha^2\beta}}{\alpha}\int_{-\infty}^{\infty}{e^{-z^2}dz}=\frac{\sqrt{\pi}e^{-2\alpha^2\beta}}{\alpha}
so we now get a differential equation (linear):
\frac{\partial I}{\partial \beta}-2\alpha^2I=-2\sqrt{\pi}\alpha e^{-2\alpha^2\beta}
Solving this (which is no big deal) we obtain:
I=\frac{\sqrt{\pi}e^{-2\alpha^2\beta}}{2\alpha}+Ce^{2\alpha^2\beta}
I(\beta=0)=\int_{0}^{\infty}{e^{-\alpha^2x^2}dx}=\frac{\sqrt{\pi}}{2\alpha} \\\\\Rightarrow C=0.
So,
I(\alpha,\beta)=\int_{0}^{\infty}{e^{-\alpha^2\left(x^2+\frac{\beta^2}{x^2} \right)}dx}=\frac{\sqrt{\pi}}{2\alpha}e^{-2\alpha^2\beta}
66An alternative:
Given
I =\int_0^\infty e^{-\alpha^2(x^2+\beta^2/x^2)}\ \mathrm dx --------- (1)
Transform the exponent as follows:
x^2+\dfrac{\beta^2}{x^2}=\left(x-\dfrac{\beta}{x}\right)^2+2\beta
using which (1) becomes
I=e^{-2\alpha^2\beta}\int_0^\infty e^{-\alpha^2\left(x-\frac{\beta}{x}\right)^2}\ \mathrm dx ------(2)
Let
I_1=\int_0^\infty e^{-\alpha^2\left(x-\frac{\beta}{x}\right)^2}\ \mathrm dx ---(3)
Apply the substitution t = βx (β needs to be strictly positive) which gives
I_1=\int_0^\infty e^{-\alpha^2\left(t-\frac{\beta}{t}\right)^2}\dfrac{\beta}{t^2}\ \mathrm dt=\int_0^\infty e^{-\alpha^2\left(x-\frac{\beta}{x}\right)^2}\dfrac{\beta}{x^2}\ \mathrm dx ------(4)
Adding (3) and (4), we obtain
2I_1=\int_0^\infty e^{-\alpha^2\left(x-\frac{\beta}{x}\right)^2}\left(1+\dfrac{\beta}{x^2}\right) \mathrm dx
Finally the substitution z=\alpha\left(x-\dfrac{\beta}{x}\right) reduces this to
2I_1=\dfrac{1}{\alpha}\int_{-\infty}^\infty e^{-z^2}\ \mathrm dz=\dfrac{2}{\alpha}\int_0^\infty e^{-z^2}\ \mathrm dz
Hence
I_1=\dfrac{1}{\alpha}\int_0^\infty e^{-z^2}\ \mathrm dz
And so
I=\dfrac{e^{-2\alpha^2\beta}}{\alpha}\int_0^\infty e^{-z^2}\ \mathrm dz=\dfrac{e^{-2\alpha^2\beta}}{\alpha} \cdot\dfrac{\sqrt{\pi}}{2}
1Hey Ricky ... the limit is between 0 and ∞ ... and not 0 and α !!!