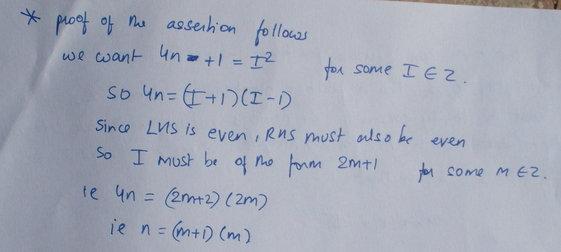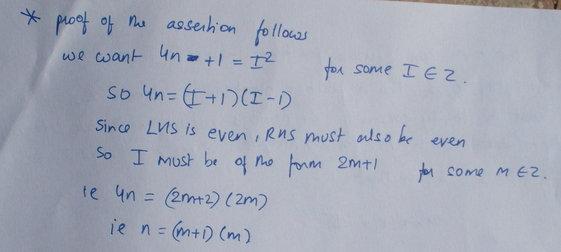21Suppose P is any non square number
Its easy to see that X(p - [√p]) = P
All integers can be expressed as (p - [√p])
Let (p - [√p]) = n
so Xn = n + [√p] = n + <n>
As [√p] = <√ (p - [√p]) > hence proved
Proof of the property
[√p] = <√ (p - [√p]) >
As P is a non square number N2<P<(P+1)2
so [√p] = N
we have to prove <√ (p - [√p]) > = N
P can be written as N2 + K where 1≤K≤2N
so we have to prove <√(N2 + K - N)> = N
This is true because for N+1≤K≤2N we have N<√(N2 + K - N)<N + 0.5
and for 1≤K≤N-1 we have N- 0.5 <√(N2 + K - N)<N
for K = N its verified that <√(N2 + K - N)> = N
So proved
341Or maybe we will present it in a such a posh manner it will look better :D.
First lets convert the <> to something we are familiar with.
note that
<x> = \left[x+\frac{1}{2} \right]
So, we look at the sequence
a_n = n +\left[\sqrt n+\frac{1}{2} \right]
Now let n=m^2+k; 0 \le k \le 2m
Its easy to prove that
m^2<m^2+m < \left(m+\frac{1}{2}\right)^2<m^2+m+1<(m+1)^2
That means
\left[\sqrt {m^2+k} + \frac{1}{2} \right] = m ; 0 \le k \le m^2+m
and
\left[\sqrt {m^2+k} + \frac{1}{2} \right] = m+1 ; m^2+m+1 \le k \le 2m
With this we easily see that the numbers
(m^2-m+1,m^2-m,..., m^2,...,m^2+m)
get mapped to
((m-1)^2+1,(m-1)^2+2,....,m^2+2m)-\left{m^2 \right}
Thus every natural number is obtained and the squares are missed
341
Hari Shankar
·2011-02-16 05:58:26
sorry, we seem to have started posting together
21
Shubhodip
·2011-02-16 07:32:50
EDIT : As P is a non square number N2 <P < (N+1)2
instead of N2 <P < (P+1)2
<x> = [x + 0.5]
this was great ..
1nice solution shubhodip and as alwayss prophet sir. my solution is also similar, posting it below.
also pls post the time it took you to think of the solution . 2hrs<me<2.5hrs
