In the plane there are n points such that of any 3 points always two points can be chosen such that their distance is less than 1. Prove that within these n points there are [n+1/2] which can be covered by a circular area with radius 1 ! [] denotes the integral part of the respective term
3heres my approach....... l
ets take 1 point as center of cirecle............
now we have to choose 2 other points.[makin pairs of 3]
................. n C 2 ................ .....
now n times same point can be chosen .............
[nC2/n] ...........................
.but we forgot to count the point itself[center of circle ............. [nC2/n +1] = [n(n-1)/2n + 1] = [n-1/2 + 1] = [n+1/2]!!!!!!!!!!!!!!!!!!!!!!
3heres a way way simpler approach.....lets take 1 point as cener of unit cirecle..........
now 1/2 ofthe remalining points will be <1 from the point!!!!![from data given]......
2 out of 3 points are <1 apart.....
if 1 is alrady chosen 1 out of the 2 will be <1 apart!!!!!!!!!
[n-1/2] points will be in unit circle...........
now we again forgot to add center of circle ........
[n-1/2 + 1].........[n+1/2]......
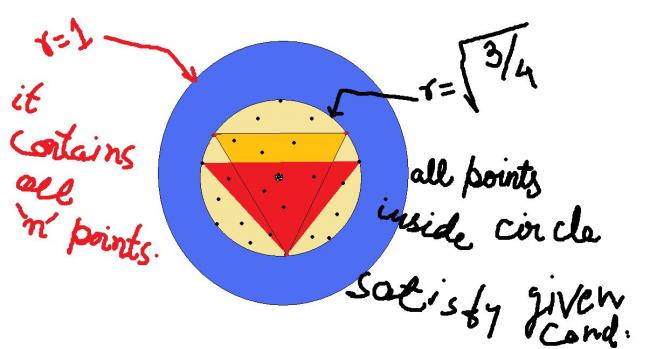
1all black dots are ...suppose the 'n' points such that of any 3 points always two points can be chosen such that their distance is less than 1.
but the circle is of radius √3/4 so the bigger circle will contain aalll of them...
.....then how the answer is only half of it......
1we had to prove [(n+1)/2] and iitimcom......has proved [n+1/2]....and u have agreed ....
.....@mathematician which 1 is correct ....if second 1 then mine must also be correct...
3how u came to a conclution that all points are inside the root(3/4) rad 1......
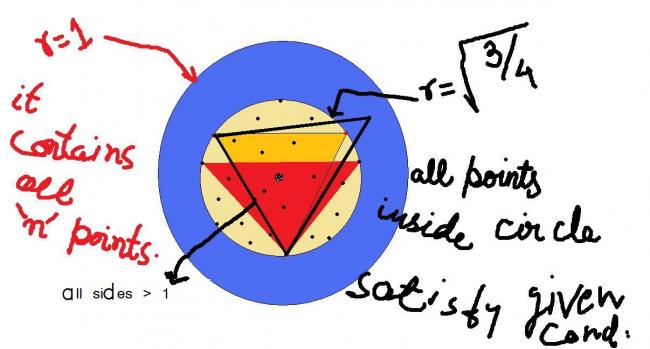
1because if we consider any point outside that circle ,then there is triangle,which have all its side length more than 1.
1i am happy taking n-1 points inside the circle and let the nth point move in infinity
@mathematics r u making questions of ur own ???????
1anyone tell me where i m wrongg?
nishant bhaiya kuch kijiye...
9let us take 2 points with distance >=1
if we draw circles of radius 1 frm these 2 pts , every other pt has to necessarily lie inside either of the circle to satisfy gvn condition
so if X pts are in 1st circle , Y pts in 2 nd circle
X+Y = n
for n even
X 0r Y >= n/2 ie >= [(n+1)/2]
for n odd
X or Y >= n+1 /2 ie >= [(n+1)/2]
hence proved :)
