i cudnt understand
Lakshya: 7:17pm 14-11-08
The question is that there is a right angled triangle ABC right angled at B. The angle bisectors of angle A and C meet at a point P. From P a perpendicular PM is drawn to AC. If the length of PM is 4root2, then find the length of BM. I get the solution when I suppose it is an isoceles triangle. Tell me is there any other way out by not supposing that or if there is no way then tell me how to prove it isoceles?
-
UP 0 DOWN 0 1 7

7 Answers
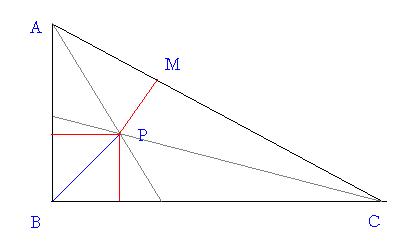
Now here P is the incenter..
so the three red sides are all 4√2
so BP=8
i think that the question is incomplete
let us join B to M
let the feet of perpendiculars from P to the AB be D
then in triangle BMP ,√BPM=√DPB+√DPM
as ADPM is cyclic √DPM=180-√A
and further √BPD=45 (as it is right angle isoceles)
so we get by cosine rule in that triangle =>
cos(45+180-A) = (BP2+PM2-BM2)/2*BP*PM
as we already know BP and PM , to find BM we need to know cos(180+45-A) => to know angle √A
but with a fixed inradius ,(that's all given in ques) we will get varied values of A
so value of angle A should be known
no there is no need for the requirement of the isoceles triangle.. check my method buddy!
Do u see that P is the incenter? (incenter is the meeting point of angular bisectors)
Once P is the incenter, It is equidistant from the 3 sides!
So the three red lines are of equal length :)
Now the blue line (THe one whose length we have to find) is the diagonal of the square of sides of length red lines)
so the length is root 2 times the length of the red lines!
OOOOOPS>.. dude i din see that!
i just thought we needed to find BP..
sorry u are right..