1yes govind is correct....... harsh, your method is wrong....
i can say that because i qualified rmo 2009......
53 Answers
11i gez it shudnt exceed 40......... bt as the paper ws easy...... now i m feeling it..... it might go to 50s even.......
it can be 13 if the book is printed only one side..............................think over it
1I solved the question using method of contradiction.
Suppose a2 - 3a - 19 is divisible by 289.
Then a2 - 3a - 19=289k for some a, k ε Z
then a2 - 3a - 19 - 289k=0 is a quadratic in a where a ε Z.
for a to be an integer, discriminant must be a perfect square.
i.e. 1156k + 85 must be a perfect square.
i.e. 17(68k + 5) must be a perfect square.
i.e. 68k + 5 must be divisible by 17.
but that is not possible.
Thus our assumption that a2 - 3a - 19 is divisible by 289 is false.
1an easy method fr ques 4......
S(odd nos.) = 111 + 113 + 115 + 117 + 119 +131 + ....... + 999
S(odd nos.) = 999 + 997 + 995 + 993 + 991 + 979 + ....... + 111
Adding,
2S(odd nos.) = 1110 + 1110 + 1110 + ........ (125 times)
Hence, S(odd nos.) = (1110 x 125) / 2 = 69375
S(even nos.) = (1088 x 100) / 2 = 54400
S(3-digit nos.) = 900 / 2 (100 + 999) = 494550
Hence, Req. Value = 494550 - (54400 + 69375) = 370775
1
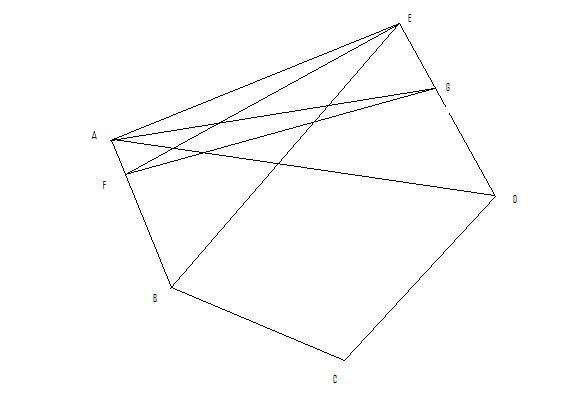
let F,G be the any two points on polygon ABCDE......
join FG, AG, FE, AD, EG... ( nearest vertices of F and G)
in triangle AEB, cevian FE<(AE+BE)/2 .......
FE doesnt exceed 1 ...... (AE and BE dont exceed 1)
also in triangle EAD, cevian AG<(AE+AD)/2 .....
AG doesnt exceed 1 .......
in a quad, all the sides r shorter than atleast one of the diagonals.......
in quad AEGF, both diagonals AG and FE dont exceed 1.....
so....... FG doesnt exceed 1.....
guys..... plzzz tell if this method is authentic or not...... shall i be getting marks fr this???
1There is a very simple and pure geometrical solution to the 1st sum
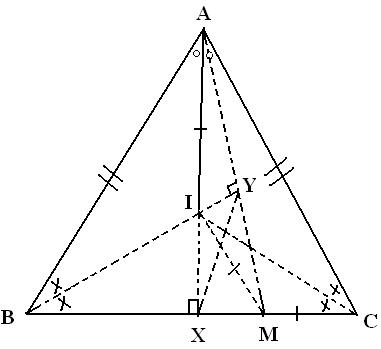
BM is taken such that BM=AB
AI is produced to make perpendicular on BC
Then the points are joined as shown by the dotted lines.
AB=BM, BI bisects <ABM, Therefore BY perpendicular on AM.
Let <ABY=<XBY=<ACI=<BCI=xo
ABXY is a cyclic quad.
Therefore <XAY=<YBX
Now <MAI=<ICM=xo
And they are on same base IM. Therefore AIMC is a cyclic quad.
Therefore <AMI=<ACI=xo (same arc AI)
Given BC = AB+AI = BM+MC
Therefore AI=MC
Equal arcs subtend equal angles at the centre
Therefore <AMI=<MAC=xo
Therefore <BAX=<CAX=2xo
And <BAC=4xo
But in Triangle ABX <BAX= (90-2x)o
By the problem,
(90-2x) = 2x,
4x = 90o
Therefore <BAC = 90o
1according to me the answer is 2
proof:-
sum of pages torn is =101
suppose first page folded is n & total number of pages folded is t
so
n + (n+1) + (n+2) + .......... +(n+t-1) =101
nt + ( 1 + 2 + 3 +......(t-1) ) = 101
nt + t(t-1)2 = 101
nt = 101 - t(t-1)2
n = 101t - (t-1)2
now n must be integer & 101 is prime number
so t only can be 1 , 2 , 101 & 202 only (if we put any other positive value of t then n comes in fraction)
when we put t = 1 then n = 101
when we put t = 2 then n = 50
when we put t = 101 then n = - 49
similarly t ≠202
so t only can be 2 because n can be 1 , 2 , 3 .....100
so pages torned are 50,51 only
tell me that my answer is wrong or correct (jindalharshkumar@gmail.com)
1i read in class X. in which class/year should i attempt to sit in rmo?
can anybody suggest?
29No Harsh ur method is not correct..i remeber many ppl whom i know did the same mistake in this question....actually wen u open up a book u will find the find the odd number pages on the right and wen u turn the page u get to see a page with an even number on the left...so if u tear pages with no. 50 and 51 ..then the pages with no 49 and 52 will also be torn off....
btw..where in the question it's given the second page is blank....the second page isnt blank....
But what if a person reads ebooks..
@Sayandas...u can attempt maths olympiad in ur class X itself..the question asked in RMO require the basic concepts that one reads in class IX and X ..but a bit more thinking process is required...there are books available for maths olympiad..u may do those books..and for some good problems on maths olympiad u may visit the maths olympiad section on this site or u may try www.mathlinks.ro : )
isit possible that the book has page printed only one side
in this case i found the possible answers may reach 13 pages : 1,2,3,4,5,6,7,8,9,10,11,12 & 23
i have written about both cases -when book has pageprinted only one side
and when the book has page printed both side
anone plz tell iam right or wrong
36Respected seniors,
The RMO 2010 is gonna be conducted on 5th of December 2010. This is me Rahul Mishra a student of Std X. I want to qualify RMO 2010. Please suggest me how should i prepare. I can not get anything of Q1, Q2 & Q3 but i don't want to give up. Please suggest me.... plz plz plz plz.....
Thankyou!
yours obediently
Rahul Mishra.....
62post your email id on my chatbox.. I will mail you a book.. read it [1]
36Loads and loads of thanks sir!
got that.....
will take a print out of it...
Hope it will be helpful...
39nishant sir ,
may i know the name of the book?
so that it would help others too :)
1see people sum of total pages is n(n+1)/2 and sum of remaining pages is 15000 . therefore if rth page is torn then n(n+1)/2 - r(r+1)=15000 solving the above diophantine equation yields no integral solution .. how is this possible....?????
1057i will also give rmo this year.....can u also plz mail me de book....i hav posted my email address on your mailbox...
215)The fifth one was unsolved here...I was trying this and so posting what i got.. its simple..
1)When we measure the distance of a line from a point the minimum distance is the perpendicular distance and maximum occurs at either of the end points of a line. So distance between two lines is maximum when the two point we choose is either of the four possible pair of points, one of which is end point of one line and the rest is end point of the other line..But none of those distances are greater than 1, according to the condition of the problem. So distance between any two points on the boundary must be smaller than 1.
2)Join X,Y and extend on either sides. Let it intersect the polygon at Z1 and Z2.The points Z1, Z2 are in opposite directions of both X and Y.. Since Z1,Z2 are in the boundary of the polygon 2|Z1Z2|≤ 2, Which means (|XZ1| + |YZ1|) + (|XZ2| + |YZ2|)≤2. So at least one of the summands in the bracket must be ≤ 1. Choose Z = Zi, if (|XZi| + |YZi|)≤ 1.
1i m an 8th grader and wen i saw these problems i had no idea abt them can anyone help me qualify for inmo next year
16 was probably the easiest ques of the paper.....
it was an simple application of ap.......
u got sum of torn page nos. = 101 after that taking least possible values, n/2(n+1)<101
which gave n=13
it meant at maximum, 6 pages cud be torn....
even no. of pages wer not possible.....
as odd x even = even
for 1,3,5
for 1 page, values wer 50,51...... (even,odd) pair..... which is not possible.... as page nos. of books are (odd,even) pairs......
then same u needed 2 prove fr 5 pages.......
hence only 3 pages satisfy every value........
hence, 3 pages wer torn........
1my solution to 4
we are required to find sum of all 3 digit nos. - (sum of all numbers with only even digits + sum of numbers with odd digits)
let us calculate the sum of 3 digit numbers with all even digits.
sum of even digit numbers between 200-300
200+220+240+260+280=1200\\ 202+222+242+262+282=1210\\ 204+224+244+264+284=1220\\ 206+226+246+266+286=1230\\ 208+228+248+268+288=1240
so sum = 6100
sum of even digit numbers between 400-500 can be obtained by adding 200 to each of the above 25 numbers
so sum = 6100+25 \times200=11100
sum of even digit numbers between 600-700 =11100 +25\times200=16100
sum of even digit numbers between 800-900=16100 +25\times200=21100
so sum of even digit numbers = 54400
let us calculate the sum of 3 digit numbers with all odd digits.
sum of odd digit numbers between 100-200
111+131+151+171+191=755\\ 113+133+153+173+193=765\\ 115+135+155+175+195=775\\ 117+137+157+177+197=785\\ 119+139+159+179+199=795
so sum = 3875
sum of odd digit numbers between 300-400=
3875+25 \times 200=8875
sum of odd digit numbers between 500-600 =8875+25 \times 200=13875
sum of odd digit numbers between 700-800 =13875+25 \times 200=18875
sum of odd digit numbers between 900-1000 =18875+25 \times 200=23875
so sum of odd digit numbers = 65500
sum of all numbers with only even digits + sum of numbers with odd digits= 119900
total sum of 3 digit numbers= 449550
so sum of required numbers= 449550-119900=329650
i think there is a calculation mistake but the method is the same
1i was getting 370775 to the fourth one . anyone else getting that? i'll post my solution to 2 and 6 later :)