1057the 4th question can be done uses the cases of even nos in that 4 digit no...
Case 1:If there is 1,3,5 and 0
total cases:3 x 3 x 2 x 1 = 18 cases
Case 2:If there is 1,3,5,(2/4)
total cases:2 x 4!=48
Case 3:two odd nos and a 0 and a even no....
3C2 x 2C1 x 2 x 4 = 48(as de even no can be placed in 4 places)
Case 4: two odd nos and 2 even nos except 0
4! - 3C2 x3 x 2 =6
total cases:18+48+48+6=120
1057Let E denotes the even digit and O denotes odd digit.
Now consider such numbers starting with an odd digit.
So the numbers are of the form OEOE,OOOE,OOEO,OEOO.
Clearly number of the numbers of the form OOOE is 3 x 3 x 2 x 1=18(same for the numbers containing only one even digit).Number of numbers of the form OEOE is 3.3.2.2=36....
So total no. of such numbers starting with odd digit is 3 x 18 + 36=90
Now consider the numbers starting with even digit:
EOEO,EOOO,EOOE
EOEO-2.3.2.2=24 ways
EOOO-2.3.2.1=12 ways
EOOE-2.3.2.2=24 ways
So total number of such numbers is 90+24+12+24=150.
12. problem 2 was pretty simple,
we have ,
2n+1=a2
3n+1=b2
as a2 is odd it is of the form 8t+1 for some int t.
then we get n=4t,
this implies 3(4t) +1 is odd so b2 is also odd.
as both a & b are odd perfect squares so they must be of the form
8k+1.
so,
2n+1=8l+1,
3n+1=8m+1,
for some l,m
form there we get,
n=4l &
n=8m/3
this implies 3|n & 8|n
so n is of the form
24j {obviously,j≠0}
now ,
5n+3=5(24j)+3=
3(40j+1)
which is clearly composite!!
211) 
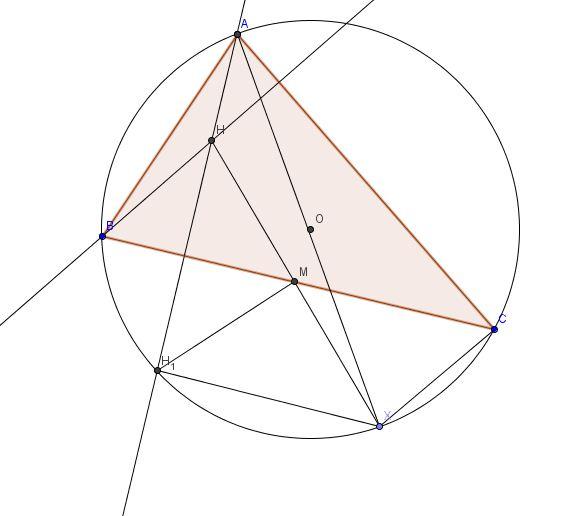
The fact I'm going to use without prove is that reflection of H on the line BC lies on the circumcircle of \triangle ABC.
Let H_1 be the reflection of H on the line BC. Let HH_1 intersect BC at T
Join AO, let it meet the circum circle at X. Join HX. Let it intersect BC at M. Equivalently we have to prove that M is the mid point of BC.
Since \angle AH_1X = \frac {\pi}{2}, BC \parallel H_1X. Since \triangle HMT \cong \triangle H_1MT, HM= H_1M = MX.
Now consider \triangle BHM and \triangle XMC.
\angle HBM = \angle XCM = \frac{\pi}{2} - \angle ACB
\angle HMB = \angle XMC
HM= MX
So \triangle BHM \cong \triangle XMC
So BM= MC , QED
21@ameyaloya : Because proving it that it can be factored is not enough
see 5 = 1*5, but 5 is a prime
You have to show that one of the factor = 1, and the other is a prime can not happen :)
212. Let 2n+1=k2 and 3n+1=l2.
So, 5n+1=(2k+l)(2k-l)
Claim: 2k-l>1...(1)
Proof:Putting k=√(2n+1 and l=√(3n+1) in (1) we get,
2√(2n+1)>1+√(3n+1)
Squaring we get,
8n+4>1+(3n+1)+2√(3n+1)
→5n+2>2√(3n+1)
Now, (5n+2)/2>√(10n)>√(3n+1)
So, our claim is true and 5n+3 is composite
1this paper was simpler than rmo 1
@ shubhodip why is my proof incomplete??
1@ vivek it would have been gud if had seen the solution......i would have got 19
marks more
21@Ketan :
Yes same question came in exam, but it's not Vivek's fault :)
@ameyaloya: The proof is a bit incomplete , though you may have left it considering it trivial :) ;)
1for the 2:
2n +1 = a^2
3n + 1 = b^2
eliminating n;
1 = 3 * a^2 - 2* b^2
so 5n + 3 = a^2 + b^2+ 3* a^2 - 2 b^2
= 4 * a^2 - b^2
= 2a- b * 2a + b
so 5n + 3 is composite
262got through 2 and 3 till now. trying the rest.
thanks for uploading :)
1057http://www.targetiit.com/iit-jee-forum/posts/find-largest-n-20203.html
same question came in de exam.....
213.Shubhodip's solution:
Case 1: a2+b2 ≥ b2+c2 ≥ c2+a2
→ b2 ≥ a2 ≥ c2
As, 1/a ≥ 1/b ≥ 1/c or 1/a ≤ 1/b ≤ 1/c, we get a=b=c
Similarly for a2+b2 ≤ b2+c2 ≤ c2+a2
we can prove that a=b=c
