1Well , the first one is rather easy .
There is a well - known identity called Bezout ' s Lemma . It states that -
Suppose , d = G . C . D . ( y 1 , y 2 , y 3 , ...... , y n )
Then we can always find such integers ( x 1 , x 2 , x 3 , ...... , x n ) for which ,
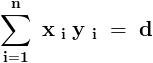
But we have ,
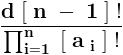
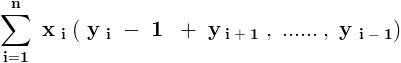
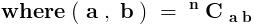
Clearly , the R . H . S . of the equation is an integral number .
Hence , the problem .
1Actually , for Qs . 3 , the easiest proof is to find a way to prove that all the points O i lie on a Neuberg Cubic , and they do so as they are Isodynamic points on the circles of Apollonius built on each side of the four triangles . But that way is too complex , so I ' ll try to find out a simpler solution .
1Well , I read that only in wikipedia :) Coz I coudn't find any book on it :(
Not that I have a sound knowledge about them , but still , this problem is based mainly on basic ideas ......
