1
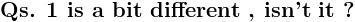
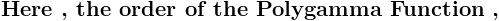
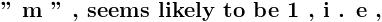
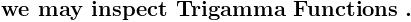
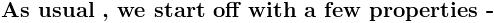
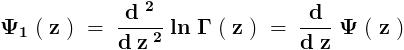
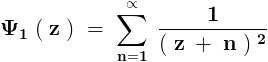
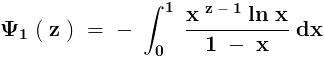
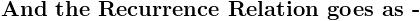
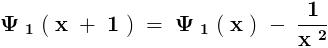
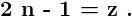
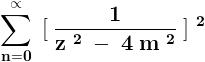
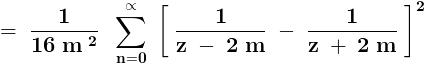
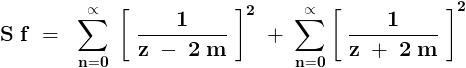
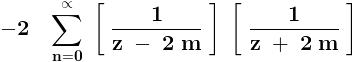
\sum_{n= 1}^{n=\infty }{}\frac{1}{\left\{(2n- 1 )^2- ( 2m ) ^2 \right\}^2}
2.\sum_{n=1}^{n= \infty}{\frac{1}{n( 36n^2-1)}}
3.\sum_{n=1}^{n= \infty}{\frac{1}{n( 9n^2-1)}}
-
UP 0 DOWN 0 1 17
17 Answers
1Actually , after that , it becomes very dirty . We have to use many other special functions to get our job done . Immediately , I can't find a simpler solution . However , I shall try . Lets see what happens .
62No one trying these?
Are these doubts or good questions to try??
39Well I have no knowledge of this stuff...you can take over from here :P
1Sorry Pritish , your method , though correct , doesn't help much due to the fact that each of the parts A , B , and C are divergent serieses , i . e , their values , each , tend to infinity .
39Q3.
{\frac{1}{n( 9n^2-1)}} = \frac{1}{n(3n - 1)(3n + 1)} = \frac{A}{n} + \frac{B}{3n - 1} + \frac{C}{3n + 1} \textup{where A, B and C are -1, 3/2 and 3/2 respectively}.
\textup{Therefore, this implies that} \sum_{n=1}^{n= \infty}{\frac{1}{n( 9n^2-1)}} = \sum_{n=1}^{n= \infty}{\frac{-1}{n}} + \sum_{n=1}^{n= \infty}{\frac{\frac{3}{2}}{(3n - 1)}} + \sum_{n=1}^{n= \infty}{\frac{\frac{3}{2}}{(3n + 1)}}
Rest can be solved as limit of a sum I think?
Same procedure for second and first parts.
