A more trivial construction, no mathematical ""thought"" necessary....
Found somewhere.. very good problem, check how trivially you can give answer.....
Is there an infinite matrix Amn such that limn→∞ amn=0 for every m and limm→∞ amn=1 for every n ?
-
UP 0 DOWN 0 1 16

16 Answers
you are right celestine.. but is it necessary that a function can be defined only if the limit exists?
the question states that its an infinite matrix
so for it to exist limit →∞ has to exist
@ nishant sir
what about m=n=inf ? amn cant be defined there !!!
I dont know to which question,you wanted reply,still,i suppose to above question in #10.
See that for matrix to exist, limit need not exist in both direction simultaneously.
In fact as an analogy to function of complex variables let f(x+iy), which takes essentially two reals as input,
limit need not exist simultaneously as x and y tend to infinity.
Existence of function doesn't necessisates existence of limit.
Here limit exist in one direction(i.e. dimension) only at a time.
As a simple example consider f(x,y)=1/(x-y).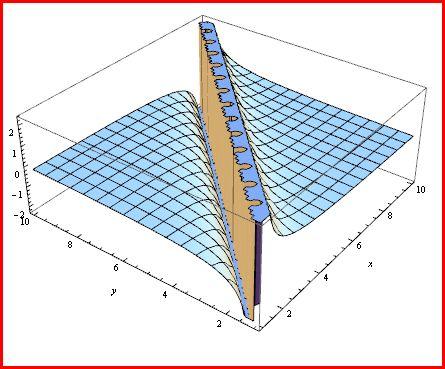
what uve posted abv is out of my understanding !
i mean wen u r taking a snapshot post the full page so that we can understand in which context the author is talking
ith power i was asking abt ur ans for abv q in #1 does a matrix exist ??
thats not a snapshot. thats a graph i myself plotted using MATHEMATICA.
aND AS I EXPLAINED, THE MATRIX EXISTS. AS FOR EXISTENCE OF FUNCTION, LIMIT NEED NOT EXIST.
FOR THE EXAMPLE ABOVE:
see as x→∞or y→∞, f→0.
But if both tend to ∞, limit of f does not exist.
but then wat will be value of amn if m,n both equal and tend to inf ???
nothing.
Why should it exist anyway?
Chech that ∞ is not a number.
\infty\not\in\mathbb{R}.
So the condition of problem is still valid.
i.e. For every n, (and that usually means for every n\in\mathbb{R}), \lim_{m\to\infty}a_{mn}=1