211) C.S inequality or Lagrange's identity
2) chebychef's inequality + AM-GM
Prove the following two inequalities : -
1 .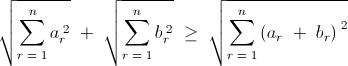 
Please note that " a r and b r " are two sequences of real numbers .
2 .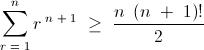 
Also infer when the two equalities hold .
Note : - The first problem has got many solutions . But the smallest I could find was my own . So it would be best if one tries this one from different angles .
Problem Source : - Problems In Inequalities - Gabriel Klambauer
-
UP 0 DOWN 0 0 5
5 Answers
21211) square both sides, and C.S does it all
2)
By chebychefs
n(1n+1+ 2n+1 +...+ nn+1)≥(1+2+3+...+n)(1n+ 2n+ ...+ nn)
further (1n+2n+...+nn)>n n!
combining them
(1n+1 + ...+nn+1)≥n(n+1)n!/2 = n(n+1)!/2
341I am a bit puzzled about the second one. Because
n > \frac{n+1}{2}, n>n-1,n>n-2,...,n \ge 2 \Rightarrow n^n > \frac{(n+1)!}{2}
so that
n^{n+1} > \frac{n \times((n+1)!)}{2}
So why summation?
3411st one is minkowski.
In vector form it is ||v_1||+||v_2||\ge ||v_1+v_2||