prove

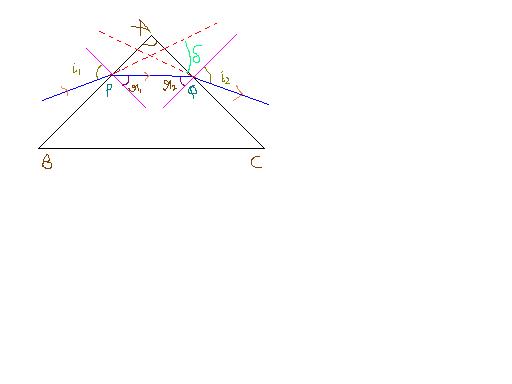
From geometry,
\delta = i_{1} + i_{2}- A

For min deviation,
\sin i_{1} = \mu \sin r_{1} and

\mu \sin r_{2} = \sin i_{2}

So, \delta = \sin^{-1} \left(\mu \sin r_{1} \right) + \sin^{-1} \left(\mu sin r_{2} \right) - A

Since, r_{1}+r_{2} =A, we get

\delta = \sin^{-1} (\mu \sin r_{1}) + \sin^{-1}\left[\mu sin (A- r_{1}) \right]

But minimum deviation arises when,
Differentiating w.r.t r ₁, we get

\frac{\partial \delta }{\partial r_{1}} = \frac{\mu \cos r_{1}}{\sqrt{1 - \mu ^{2}\sin ^{2}r_{1}}} + \frac{\mu \sin (A-r_{1}) }{\sqrt{1- \mu ^{2}\sin ^{2}(A-r_{1}})} = 0

\frac{\cos r_{1}}{\sqrt{1-\mu ^{2}\sin ^{2}r_{1}}} = \frac{\mu \cos r_{1}}{\sqrt{1-\mu ^{2}\sin ^{2}(A-r_{1})}}

Since, internal reflecting angles are same in the condition of min deviation, therefore, r_{1} = r_{2}=A/2

on putting in the above equation, we get

i_{1} = i_{2} = i

Therefore, thus proved.