A≈0
B=attractive
C=minimum
D=repulsive
The ideal gas model assumes that there are no interactions between gas particles. Particles in a real gas do interact through a range of forces such as dipole–dipole forces, dipole–induced– dipole forces, and van der Waals interactions (induced–dipole–induced–dipole forces). A typical curve showing the potential energy of interaction between two particles is shown below.
What is the force at the four points marked A, B, C and D on the figure?
(attractive / repulsive / approximately zero)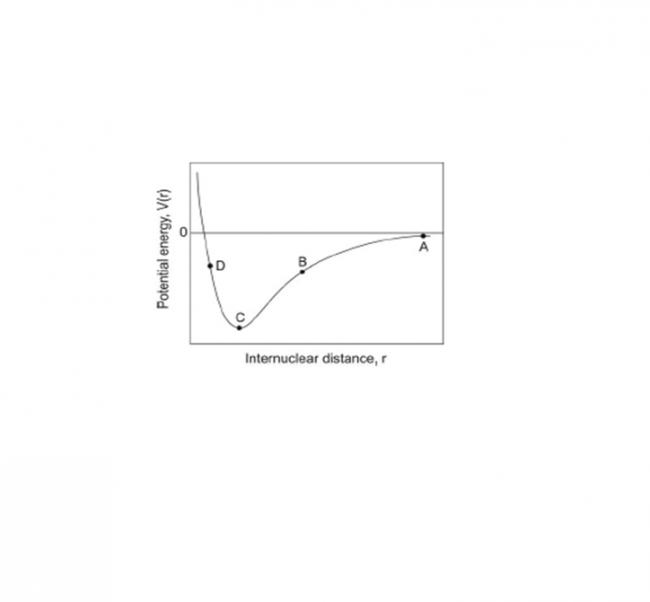
-
UP 0 DOWN 0 2 10

10 Answers
Yes, Eureka you're correct.
Can you explain a little bit on why this is the resultant graph?
In the meanwhile, let me give one more question:
Q) The deviation from non-ideality in a gas is often quantified in terms of the
compression ratio,
Z = (Vm)/(Vo)
where Vm is the molar volume of the real gas, and Vo is the volume of the ideal gas under the same conditions of temperature, pressure etc.
Match the following values of Z with the dominant type of interaction in the gas.
[ Z = 1 ] [ Z < 1 ] [Z > 1 ] with -
Attractive forces dominate
Repulsive forces dominate
No intermolecular forces, ideal gas behaviour
At A distance between particles ≈ ∞ ... hence P.E =0
At B nucleus of one atom attracts electrons of the other .... attractive.
At C : P.E becomes minimum
At D : Nucleus-nucleus repulsion
Correct Aveek.
Can you answer the next question on the Compression Factor?
I am applying a bit of guess work here :
Attractive forces : Z<1
Repulsive forces : Z>1
3rd case : Z=1
Z = PV/nRT for real gases
For P=1 atm and T=273 K
V ideal = 22.4 L
If Z>1 then V (real) > 22.4 l
So, repulsive forces dominate
Similarly, Z<1 => attractive forces dominate as real volume is less than ideal volume
Z=1 => ideal behaviour
for ideal gas pv=nrt
for real gases ,pv=znrt
v=znrt/p ...............................(i)
when attractive forces dominate,v>nrt/p as volm of gas liquified will
be more than expected(ideal)
so to maintain the equation the eqn (i) z<1
conversely when repulsive forces dominate v<nrt/p.so to maintain eqn(i) ,z>1
for ideal behaviour v=nrt/p.putting this in eqn(i) z=1
Good, I am satisfied with the answers and their explanations as well :)