its nowhere written that the central large sphere is hollow and y did u take R=10r
If a cube is made such that small spheres are at the corners and large sphere is at the body centre of the cube, then what is the packing fraction of this system?
1. 0.68
2. 0.74
3. 0.52
4. 0.002
-
UP 0 DOWN 0 4 22

22 Answers
ya,
then it may be
because ,otherwise the question was not clear
well.
Good that this post infact cleared my many other doubts in Solid State
Thanks everyone:)
Ya Pratik this is actually a qs from a comprehension
I had a doubt to use the general P.f. & so i posted
Consider a large hollow sphere of radius "R" in which small spheres of radius "r" has to be placed in closest packing( assume r=R/10)
If a cube is made such that small spheres are at the corners and large sphere is at the body centre of the cube, then what is the packing fraction of this system?
(A)0.68 (B)0.74 (C) 0.52 (D)0.002
Now do the sum............
the diagram has given a completely new angle to da problem... as hcp is not working guess yu should start from da basics... can yu pl paste da exact wordings of da question as HOLLOW sphere is something i cant relate to. even then if yu say tht there is an imaginary (hollow) sphere and small spheres around,how are they packed??(does da question give hcp?if it does, i see a contradiction to da dimensions given) pl put the passage here...
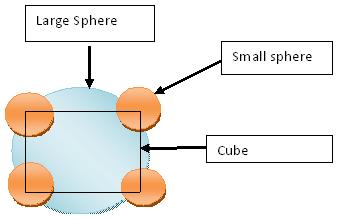
If the diagram is as given by Ashish ,
then there may be two cases :
1) large sphere is hollow
2) large sphere is solid
if large sphere is hollow then answer must be 0.002.
if not then there is a problem because ,
p.f = 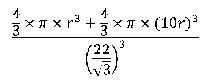
will be greater than 1.
which can not be.
it may be 1 but for that case ,
otherwise question is not clear.
post the full paragraph here. if otherwise.
well.. this was a ques from aakash aits.. so I and Uttara know the complete ques (as it was a paragraph type) which mentions that the large sphere is hollow and its radius R = 10 times the radius of the smaller spheres..
even then (i slightly doubt) there is something wrong with my method.
Here bcc formula that a√3=2(r+R) CANNOT be applied. (as then the large sphere (for R=10r) will not remain completely inside the cube

why is R=10r??
my soln:
if u take spheres at corners to be negligible and that da central sphere is very large fitting completely in da cube then:
a=2R
PF=vol of central sphere / vol of cube
=(4/3)pi R3a3
hence, pf=0.52
option(C)
the two spheres are of different radii and so R=10r cannot be taken.
if we conder it as a spherewhich is solid
the two radii being r & R then by approaching as in bcc n taking
a√3=2(r+R) n applying formulae the p.f. comes as
√32*pi
which is equal to somthing like 2.7
so either the sum is wrong or else it has to looked at with a different view
but the other structures doesnot satisfy the given data
so uttora should re chek her sum
(D) 0.002
Packing fraction depends on the volume (solid volume).. So contribution of hollow sphere to the PF is negligible
So total volume of smaller spheres in the cube = 8*1/8 (corner atoms so contribution of each to one unit cell = 1/8)*Vsph = Vsph
Now as it can be treated as BCC,
a√3 = 2(R+r)
So u can get volume of cube as a3
PF = total volume of smaller spheres in the cube/volume of cube
putting the values and taking R=10r
we get PF = 0.002
When 0.68 packing fraction was calculated,,all spheres were of same size,,here its not,,so ans is bound to be different,,and to find it we have to go from the basics like asish did.
yes,in lattice structure it were drawn as points.
but actually structure will lok like
please answer
Are the spheres in a hcp structure always linked to each other??
in bcc we have all the spheres were of same size that is they have the same size.But here it is different.Wat asish did is perfectly rite,and i cant understand wat he means by hollow.
@Uttara: BCC waala answer is valid ONLY when the body centre sphere is completely solid.. Here the body centre sphere is NOT completely solid (it is hollow) so you have to work from the basics only
@Asish This method I have seen in soln But for a BCC structure P.F. is 0.68 na??
& this is clearly a BCC