No one??
A comet is moving in a parabolic path around the Sun in the same plane as the orbit of Earth (without any collision with the Earth, obviously!). Determine the maximum time that this comet can spend within the Earth's orbit, which is assumed to be circular. Given that the time period of Earth's revolution around the Sun is T0.
P.S.: Consider the situation in which the parabola meets the circle only at two points, something like this: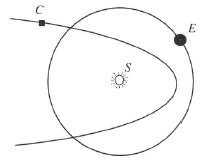
-
UP 0 DOWN 0 5 9

9 Answers
sab gayab ho gaye kya ?? let this thread come alive guys ..!
a helpful hint : As the path is a parabola , the total energy of the particle will be zero
hey this is easy ! ..
As total energy of the particle is zero .. we have -GMm/r + mv2/2=0
thus
v2/2=GM/r
v2=(2GM/r)
now let the distance of the comet from the sun be .. let say r0 and its velocity be v0
we have then mvtr=mv0r0 (angular momentum conservation :) )
now ,... oh yeah vt is the tangential velocity at any point ..
further v2=vt2 + vr2 (vr is the radial velocity of course )
vr2 = (dr/dt)2
so we have a differential equation as
(v0r0/r)2 + (dr/dt)2=2GM/r
dr/dt= √(2GM/r - (v0r0/r)2)
we integrate from R to r0 and then find the time and multiply it by 2 ..
easy ...
one small typo r0 and v0 are the things when the comet is closest to the sun
actually the basic equation is wat rohan has given
since its a parobolic trajectory we have binding energy 0
so we have
\frac{GM}{r}=\frac{v^2}{2}
everwhere !
r1is earth's orbitol radius , we have its realtion with the time period T
now at any instant r , let the velocity be v
we have
v_{radial}=\sqrt{v^2-v_t^2}
also we know that angular momentum is conserved
so
v(t)=v(0)r(0)/r
putting that in eauation
also jsut now we showed relation b/w v and r
put that i9n equation too
also
v(r)=dr/dt
hence we get this differential equation !
\int_{r_1}^{r_0}{\frac{dr}{\sqrt{\frac{2GM}{r}-\frac{v_0^2r_0^2}{r^2}}}}=\int_{0}^{\frac{t}{2}}{dt}
r_1=\frac{TR\sqrt{g}}{2\pi}
we also have
\frac{GM}{r_0}=\frac{v_0^2}{2} \\ \text{hence we can obtain T purely}\\\text{ as a function of r(0) and then }\\\text{diffrentiate w.r.t }r_0 \text{to get the answer }
More or less this problem has been solved. However, just for the sake of completeness, I shall solve it.
The total energy of the comet + sun system is zero. So we get, at any r,
\dfrac{1}{2}m(v_r^2+v_t^2) -\dfrac{GM_\odot m}{r}=0 ------ (1)
where M_\odot is the mass of the sun, vr is the radial velocity and vt is the tangential velocity of the comet.
This is a two dimensional problem. However, we could reduce it to one dimensional problem by introducing the angular momentum which is a conserved quantity in any central force problem.
Since, L=mrv_t, equation (1) transforms to
\dfrac{1}{2}mv_r^2 + \dfrac{L^2}{2mr^2}-\dfrac{GM_\odot m}{r}=0
Further, if we denote the distance of closest approach as p, then using the fact that at this point v_r=0, we get from (1) that
\dfrac{L^2}{2mp^2}=\dfrac{GM_\odot m}{p}
i.e. \dfrac{L^2}{2m}=GM_\odot mp
So after some manipulations, equation (1) ultimately becomes,
v_r^2=2GM_\odot \left(\dfrac{r-p}{r^2}\right)
If we denote the total time as \tau, then in time \tau/2, the comet moves from r=p to r=R, the orbital radius of the Earth. Using the fact that vr = dr/dt, we get
\sqrt{2GM_\odot}\int_0^{\tau/2}\mathrm dt=\int_p^R \dfrac{r}{\sqrt{r-p}}\,\mathrm dr =\dfrac{2}{3}R^{3/2}\left(1+\dfrac{2p}{R}\right)\sqrt{1-\dfrac{p}{R}}
i.e.
\tau =\dfrac{4}{3\sqrt{2}}\dfrac{1}{2\pi}\sqrt{\dfrac{4\pi^2}{GM_\odot}R^3}\left(1+\dfrac{2p}{R}\right)\sqrt{1-\dfrac{p}{R}}
Expressed in terms of Earth's time period of revolution T = 1 yr, we get
\tau =\dfrac{2}{3\pi\sqrt{2}}\cdot T \cdot \left(1+\dfrac{2p}{R}\right)\sqrt{1-\dfrac{p}{R}} -------- (2)
So basically we need to maximize the quantity
\left(1+\dfrac{2p}{R}\right)\sqrt{1-\dfrac{p}{R}}
Calling p/R = x, we need to essentially maximize
f(x)=(1+2x)\sqrt{1-x}\qquad \forall \,x\in [0,1].
Now according to AM-GM inequality
4f^2(x)=(1+2x)^2(4-4x)\le \left(\dfrac{1+2x+1+2x+4-4x}{3}\right)^3=8
So f(x)\le \sqrt{2},
the equality being attained when x=1/2 i.e. when p=R/2
And hence from (2), we obtain that
\tau \le \dfrac{2}{3\pi}T
So the maximum time that comet could spend withing the Earth's orbit as shown is
\boxed{\tau_\mathrm{max}= \dfrac{2}{3\pi}T\approx 77.5 \ \text{days}}