1V°/2?
The cube shown below has 5 faces grounded. The sixth side, insulated from the others, is held at a potential V0. What is the potential at the center of the cube and why?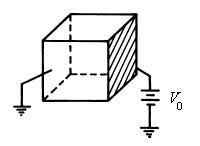
-
UP 0 DOWN 0 4 10
10 Answers
62oops Vo/6 ?
I seem to have grounded one and kept 5 at potential Vo
62The resistance between the center and each face is equal
So we have 5 equal resistances connencted between 0(ground) and V and another between V and V0
Where V is the unknown...
now it is a simple KVL problem :)
*waise to be true.. the first time i saw this question I was clean bowled! I had no clue.. but suddenly the idea stuck
66Hmm... that's good. I, however, had superposition in mind. The point is that the potential at the center must be a linear superposition of the potentials of the different faces. So that
Vc = Σ αi Vi
where Vi is the potential of the i-th plate and αi are scaling constants. Since all the plates are located symmetrically w.r.t. the center, so there is no reason to believe that any of the αi's are different; they must be the same so lets call all of them α. So
Vc = α Σ Vi.
Next, if all the plates were at the same potential, say V, then the potential at the center is obviously V, hence α = 1/6.
So we finally obtain
Vc = 16 Σ Vi
For the present case, only one of the Vi's is non zero (equal to V0) and rest zero. So we get
Vc = 16 V0
62<div><object style="width:420px;height:272px" ><param name="movie" value="http://static.issuu.com/webembed/viewers/style1/v1/IssuuViewer.swf?mode=embed&layout=http%3A%2F%2Fskin.issuu.com%2Fv%2Flight%2Flayout.xml&showFlipBtn=true&documentId=100708062847-4f79c4a187d54cf18b9a6bfb22b7c3f1&docName=logarithm_for_iit_jee&username=nishantsah&loadingInfoText=Logarithm%20for%20IIT%20JEE&et=1278570789991&er=81" /><param name="allowfullscreen" value="true"/><param name="menu" value="false"/><embed src="http://static.issuu.com/webembed/viewers/style1/v1/IssuuViewer.swf" type="application/x-shockwave-flash" allowfullscreen="true" menu="false" style="width:420px;height:272px" flashvars="mode=embed&layout=http%3A%2F%2Fskin.issuu.com%2Fv%2Flight%2Flayout.xml&showFlipBtn=true&documentId=100708062847-4f79c4a187d54cf18b9a6bfb22b7c3f1&docName=logarithm_for_iit_jee&username=nishantsah&loadingInfoText=Logarithm%20for%20IIT%20JEE&et=1278570789991&er=81" /></object><div style="width:420px;text-align:left;"></div></div>
This is a test
<div><object style="width:420px;height:272px" ><param name="movie" value="http://static.issuu.com/webembed/viewers/style1/v1/IssuuViewer.swf?mode=embed&layout=http%3A%2F%2Fskin.issuu.com%2Fv%2Flight%2Flayout.xml&showFlipBtn=true&documentId=100708070951-ddc6578c593d46868865da5f93a9f56e&docName=logarithm_and_exponentia_functions&username=nishantsah&loadingInfoText=Edudigm%20Logarithm%20and%20Exponential%20functions&et=1278573251763&er=4" /><param name="allowfullscreen" value="true"/><param name="menu" value="false"/><embed src="http://static.issuu.com/webembed/viewers/style1/v1/IssuuViewer.swf" type="application/x-shockwave-flash" allowfullscreen="true" menu="false" style="width:420px;height:272px" flashvars="mode=embed&layout=http%3A%2F%2Fskin.issuu.com%2Fv%2Flight%2Flayout.xml&showFlipBtn=true&documentId=100708070951-ddc6578c593d46868865da5f93a9f56e&docName=logarithm_and_exponentia_functions&username=nishantsah&loadingInfoText=Edudigm%20Logarithm%20and%20Exponential%20functions&et=1278573251763&er=4" /></object><div style="width:420px;text-align:left;"></div></div>