106you can always write the differential equation and solve it [3]
I guess this is pretty tough for many guys out there -- but yesterday I learned such a great sum
that I cannot resist to give it ----------------------
Suppose you don't know any of the equations that are used in S . H . M . But you have to find out
the time period of a simple pendulum with length " l " , assuming ideal conditions .
What will you do ????????????????????????????????????????
PLZZZZZZZZZZ don't rebuke me afterwards if the solution is too tough :):):)
PS ---- I will post the solution one hour later if nobody is interested :(:(:(
-
UP 0 DOWN 0 0 15
15 Answers
106
1using the eqns of motion only for a pendulum with a mass of bob - m
and length L when released from an angle of θ0
we can easily get the expression for time period as
T=4\sqrt{\frac{l}{2g}}\int_{0}^{\theta_0}{\frac{d\theta }{\sqrt{cos\theta -cos\theta _0}}}
for very small θ0 this gives the known time period of a simple pendulum for small oscillations..
i dont know if you meant this..for this is quite a well known expression
1GREAT WORKS DUDES ---------- but I really meant something else ---------- which is pretty easy once
you understand the concept --------- and a little diffrentiation is all it takes ----------
SMALL HINT ---------- does anyone know about the LAGRANGIAN of a system ?
1The principle of least action is way out of syllabus... so maybe not now..
besides it provides just another route to the answer ...at times easier... the eqn we get after solvin the langrangian can usually be got using simple force equations
1maybe you can post it for the rest of the lot.....
for people like eure, ashish and others have finished their syll ages ago...
49Under conditions that are given in Lagrangian mechanics, if the Lagrangian of a system is known, then the equations of motion of the system may be obtained by a direct substitution of the expression for the Lagrangian into the Euler–Lagrange equation, a particular family of partial differential equations.
source:wikipedia
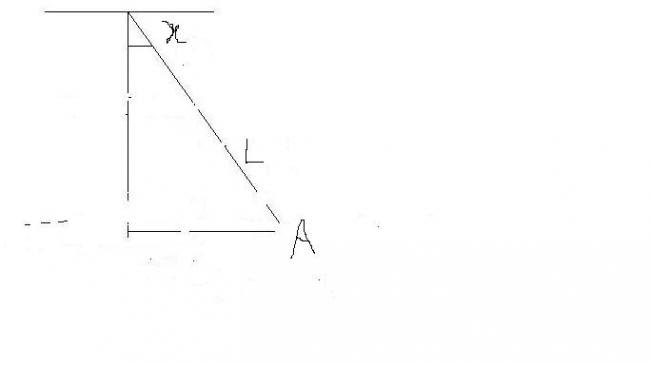
1Absolutely marvellous quotes . Subho and all the others -- the exact solution is howver as follows --
Suppose the bob of the pendulum is displaced by an angle x as shown in the figure .
K . E . of the pendulum at the point A = 12 m ( l dxdt ) 2 =12 m ( l x1 )2 , where x1 stands for the
derivative of x w.r.t time .
P . E . = m g l ( 1 - cos x )
Hence the lagrangian is given by L = 12 m l 2 x12 - m g l ( 1 - cos x )
According\; to\; the\; Eulerian - Lagrangian \;equation ,
\frac{d}{dt}\;[\; \frac{\partial }{\partial x_{1}}( L )\;] \; = \; \frac{\partial (L)}{\partial x}
Accordingly , we get \frac{d}{dt} \;[\;\frac{1}{2}\; . 2 \; .\; m\; l^{2}\;x_{1}\;] = m\;g\;l\;sin x ------------ 1
Let x2 stand for the second derivative of x w.r.t time .
So we derived that m\;l^{2}\;x_{2} = - \;m\;g\;l\;sin x
Sorry I didn't include the minus sign in eqn 1.
or x2 = - gl x
But x2 is the accelaration of the system .
So t = 2\pi \;\sqrt{\frac{length}{|accelaration|}} = 2\pi \;\sqrt{\frac{x}{\frac{g}{l}x}} = 2\pi \;\sqrt{\frac{l}{g}}
66You don't require any fancy names. What you are asking could be easily obtained by energy conservation: The total mechanical energy of the bob+Earth system remains conserved (why?)
So we get at any \theta,
mg\ell(1-\cos\theta)+\dfrac{1}{2}m\ell^2 \dot{\theta}^2=\mathrm{const}
Differentiating w.r.t. time, we get
g\sin\theta \dot{\theta}+\ell \dot{\theta}\ddot{\theta}=0\quad \Rightarrow\ \ddot{\theta}+\dfrac{g}{\ell}\sin\theta=0
Using small angle approximation and using ω2 = g/l, it finally reduces to the shm equation
\ddot{\theta}+\omega^2\theta=0
1@Soumya : see there...
as I said the same eqn can be got by methods you knew before...
66Generally, a time derivative (i.e. differentiation w.r.t. time) is denoted by putting a dot over that variable.