21Sorry [2]
if u want , i will delete it [1]
A belt is fit around the equator.
Suppose it was 1 meter extra in length, and it was lifted till it was no longer slack.
How high above the Earth's surface would you then be?
A diagram is made here:
Assume: Earth is sphere of radius 6400 km
-
UP 0 DOWN 0 0 32
32 Answers
49so h=-R+√(4R2+1)/2≈0
bt u said dat we will b shocked 2 see the answer....n this is obvious...
62there is a solution to the thing on the net to every question in the world i guess :P
But try to avoid arbitrary google search.. it is nto going to help you. Not at all. Sorry if i am being rude.. you should try these questions on the book not on google search :D
21actually i got this soln from the net , but skipped some calculation part
62not a very difficult one.. but how did you get the final result?
21
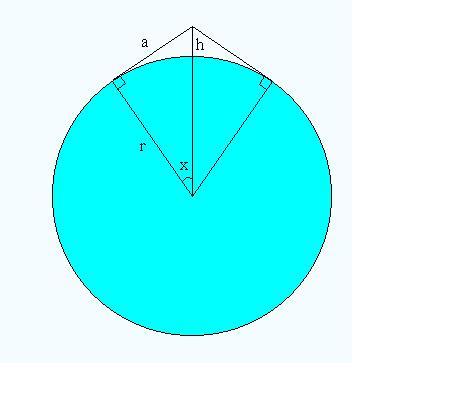
In the diagram below, the belt meets the Earth at a tangent, and therefore the angle between the belt and a radius is 90°. Consider two lines: one joining the center of the Earth to the high point of the rope; the other joining the center of the Earth to one of the points at which the belt meets the Earth. Let x be the angle subtended, in radians, between the two lines. Let a be the distance from the high point of the rope to a point at which the belt meets the Earth.
For d = 1, r = 6,400,000, we obtain h =121.6 meters.
1um ..
I was thinking all the time that it was a physics question.
62{(θ R + 1)/2}2 +R2 = (R+h)2
and
tan θ/2 = {(θ R + 1)/2}R
Now can you solve these?
62no the answer is atleast a few hundred times more than 1 meter (did i say atleast?)
24hmm
so i was wrong...
I had a bad feelign abt that ....[3][3]
btw just wondering if this ques is related to ques here
http://targetiit.com/iit-jee-forum/posts/gud-combination-of-concepts-1992.html
I mean anything to use ???
1But y is it not half????[7]
We can consider two tangents to be drawn from point O at A and B.
So AO=BO=1/2...
Sorry if its a stupid question!![14]
62but what eureka has done is incorrect..
That length is not half!!!
3it seem to me a rolling motion.Or the earth is rotating abt the pt of contact of the thread which is vertical.
62The radius of the earth is not changing..
The belt is being pulled so that it is not slack..
So there will be a height .. The question is to find that height..as shown by eureka in post 6 (diagram)
21sir can u jus see wats wrong with ma answer.......may be i may not to able to understand the q properly
62yes Dc you are on the right track.
You guys will be surprised to see the right answer ;)
1Sir u hv told that the wire is 1 m extra in length ..
So isn't it that
[ AO+OC] - [Lenght of arc AC ]= 1 m
[See euro's diagram ]
62Sorry my mistake.. it is AOC... (The diagram I made had a small issue :( )
THat is why you guys got confused
23i think nishant sir has said dat
length\; of\; wire\; = 2 \pi (64 \times 10^{5} ) + 1
