03-09-09

no one trying ??

Let f₁= ax+b and f₂= cx+d
As f₁ and f₂ are onto,

-a+b=0
a+b=k
-c+d=k
c+d=0

Solving, we get f₁ and f₂ as
y=k/2(x) + k/2 = f₁ and
y=-k/2(x) + k/2 = f₂

From graph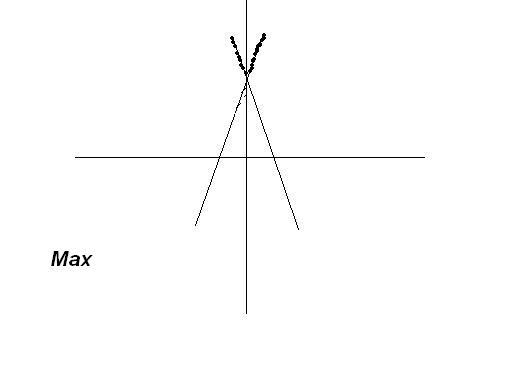

what is c and d u have taken ??

also k has to be eliminated ..

so ur ans is not rite..

c and d are arbitrary constants..
And about k, .... :(

and hint:
dont assume f₁x) and f₂(x) separately..instead generate them from a single equation f(x) using the conditions

OK..seems like some one is tryign the ques...

so i will drop a hint

Let f(x)=ax+b
Now use the condition of onto mapping from [-1,1] to [0,k]
and find values of a and b in terms of k

can we assume f₁(x) and f₂(x) as y=x and y=-x respectively.

No

Looks like everyone has given up on this