13bhaiya how to solve this question.....
Find the probability that 4 randomly chosen numbers in [0,1] are such that the distance between them is less than 1/2
any hint.....
any alternative way...other than 4 dimensions
Find the probability that the points two randomly chosen numbers in [0,1] are such that the distance between them is less than 1/2
If you remember a similar question of time that two friends meet you can solve it in a flash
Then try to solve the question that 3 points are given.. probability that all three have distance between them as less than 1/2!
-
UP 0 DOWN 0 0 28
28 Answers
62If you dont want / cant solve by finding the figure then do one thing
take a fixed value of z and find the area of the layer
then integrate..
1313try to find area of that shaded area in terms of z....length of the red line is (0.5-z)
21Abhi, can u pl. xplain ur Integration expression in mor detail!!! i dint get it [2]
13but is it possible??...4 dimension case seems interesting[12]
any alternative way....??
62@abhirup..
there is a generalization to n dimensions..
but I am sure that it will be very difficult to first visualise and then solve it for even the 4 dimension case..
13Then.....
how to find the probability if more than three points are chosen....
we don't have more than three dimensions[7]
[12]
62Yes then it seems to be awesome :)
let me do the final calculations to see if our answers do match :)
13i did 2*∫...that....dz
as the lower part and upper part has same volume....
62abhirup explain this.. why is z integral in your expression only between 0 and 1/2??
13
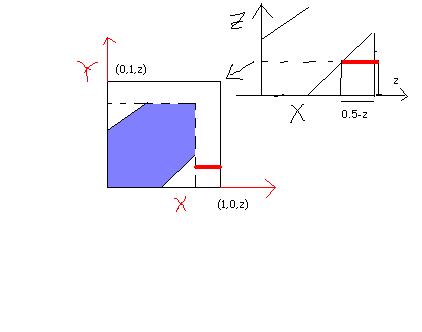
the area of the shaded layer....[0.5+z]2-(1/2)*2z2
13is the ans 1/2[7]
2\int_{0}^{0.5}{[(0.5+z)^2 -z^2}]dz
62PS: Inspired from http://targetiit.com/iit_jee_forum/posts/probability_donno_if_already_done_3248.html
21yah matie..... sample space to pata chal gai........
I m struggling to find da shape of the FAVOURABLE CASES volume
39Take the cube with one corner [0,0,0] and another [1,1,1] with side , parralel to axes. Now any point in this cube correspond to a choice of 3 points on the segment [0,1]
21INTERESTING [12]
KABHI LOCUS IN 3-D ke bare mein zyada socha nahi.....
62now how do you generalise to the 3 variable case where we have each of
|x-y|<1/2
|x-z|<1/2
|y-z|<1/2
21can u pl. add/explai the range of values our two chosen numbers can take......
13bhaaiya...can u give the link of that one....
62do you guys remember that problem where we did that 2 friends would come and stay for 15 minutes.. between 5 to 6 PM?
This has a very similar logic! (If you can feel that!)
21Can u pl. xplain this que : as in wats da range of values of pts. (in terms of dis. b/w em etc.)
Then try to solve the question that 3 points are given.. probability that all three have distance between them as less than 1/2!
21Is the ans to this : Find the probability that the points two randomly chosen numbers in [0,1] are such that the distance between them is less than 1/2
= pi(0.5)2/ pi(1)2
= 1/4 [7]