1post the ans
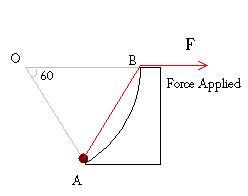
Find the work done in pulling the ball from the situation shown in the figure to the topmost point of the wedge. The wedge is immovable.
At the top there is a small pulley kind of a thing.. we dont have to worry about that. The bottomline is that the direction changes!
Assume No friction!
Mass of ball is M
Radius of the large wedge is R
Radius of the ball is negligible!
-
UP 0 DOWN 0 1 29
29 Answers
1I got your point so the correct solution will be after removing mgcos(theta) in my previous integration term
62see u need to find the work done by the Force on the string "F"
why should u bring it normal reaction or the mg component?
Did u get my point?
The remaining method is correct :)
1Hey nishant I joined new I am Himanshu's friend.
I got the soulution
We just calulate the force in the direction of the plane and integrate it as
pi/2
∫[Fsin(theta)-mgcos(theta)]Rd(theta)
pi/3
where I have taken theta to be the angle from the perpendicular.
62@sky... why? could u elaborate!
@himanshu.. ur analysis is quite good.. but u need to work more :)
1here the component of tension along the plane at all angles will accelerate the ball and so along the string the component of tension and the normal reaction must provide the centrepetal acceleration. So the normal reaction must change accordingly so that it supports the acceleration as well as takes care of mg.
1Y CANT WE TAKE IT THE OTHER WAY LIKE
(force along the direction of displacement).(displacement) ?????
1You mean the work done on the mass is same as work done on the system and since the displacement of point of application of force = R and is in dir of force it is F.R ?
62Arrey this is very simple..
I dont know if u guys were taken aback!
See the problem with the solutions that u guys posted (say aman)
The one Aman did.. if u replaced the curved surface by a plane line the work done would have been F.(AB) (RIght?)
The convensional method would have been something of the kind SkyGirl did in the 2nd post!
But it was a solvable method.. but very clumsy.. isnt it?
33Work done by a force is F multiplied by the displacement of point of application of force.....
This becomes more imp when body is like that of sponge... When u apply a little force, sponge does not move but it compresses so force does some work as point of application of force moved.....
62
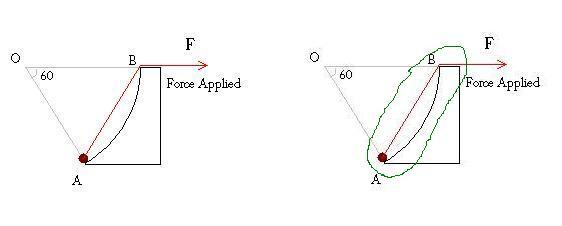
Take the green rounding as a hint!
And try to find the work done of that as a system!
I mean the string with the mass!
Now it should be simple! (Why will this be the same as the work done on the mass?!) again a simple question :)
What is the direction of the force on the new system.? what is the force on the new system.? what is the displacenemt of the point of application of the force in the new system... each one is very trivial individually..
But overall it gives such a brilliant solution! Doesnt it :)
1
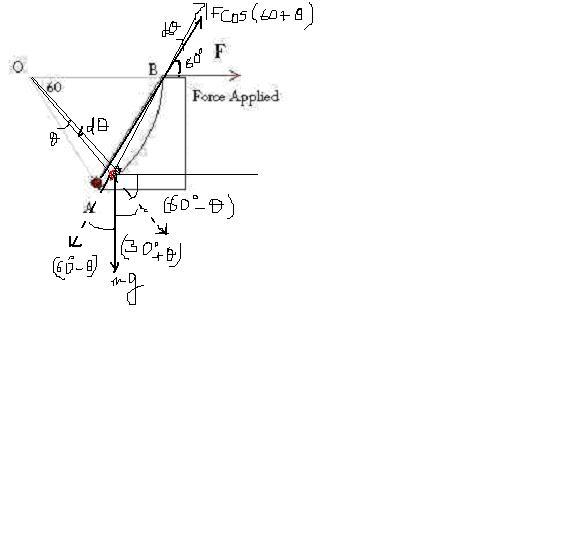
∫dW = ∫Γ.dθ
= 0∫π/3[Fcos(θ+60)-mgcos(60-θ)]R.dθ
should we proceed like this ?
62isnt it just f.(disp parallel 2 f)=f.R......(since r<<R)
No, this is not the logic! then just imagine the case: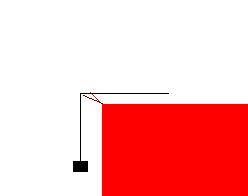
will the work be 0?
btw is the displacement parallel to f--- R? i thought it is R/2 in this case?
I guess this answers both Aman's and sreeta's doubts!
*Do u guys think i should post the answer already? or u still want to think some more?
1I think the force in every part of string is F. So, the force parallel to displacement will be F and net work done = FR/2
is it wrong ?
62work here will also be f.r!
i will tell u why!
is the work in the direction of force actually F/2
1
i have a different answer, surely its wrong. plz correct me
work done by force F will be same when the curve AB will be a straight line then component of force parallel to displacement = F/2
displacement AB = R
net work done = FR/2
PLZZZ... CORRECT ME
62Yeah .. cool.. gr8 work priyam :)
(Now i am sure u got it correct :)
33Yeah got the method, just the basic def of work, right!
Really one line! :)
62no the problem with energy approach is that we dont know the final kinetic energy.. we do know the potential energy but that alone is not sufficient!
Stay here for just 2 odd hours.. it is a one line solution!! (U will be amazed by the brilliancy and simplicity of the proof!)
62yes Priyam.. it is FR (good work..)
I think if u wrote just the answer.. u have the way as well :)
sorry ankit not mgrcos30!
The kinetic energy would hae changed by them!
62no!
this is the first way.. but i think i would not have given as the question of the day if this was the actual solution :D