am i right
This is a very famous problem of Mathematics (Not very much in IIT Syllabus though! but a very very interesting question of Limits!)
A man Starts from his home to office. When he reaches half way he starts to go back to his home. Again half way through the remaining (Returning distance) decides to go back to his office. Again half way through back to his home and so on and so forth for very large time!
Where will he be when this limit tends to infinity!
If home is at x=0 and office at x=1
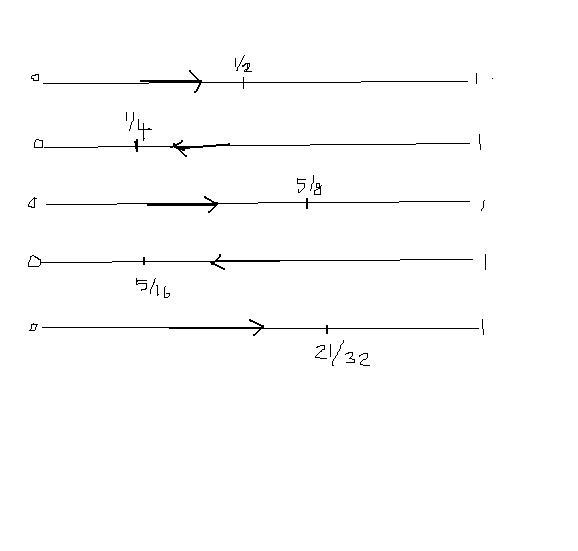
then at first return he will be at x=1/2
then at 2nd time at x=1/4
then at x=5/8
then at x=5/16
as so on and so forth!
If u cant find this limit! then what will be the behavior of this person? (Can u safely assume that he is mad? :P)
-
UP 0 DOWN 0 2 15

15 Answers
Clarification!
Home at x=0
Office at x=1
He goes from Home to office. Midway is at (0+1)/2 = 1/2
Then returns to the Home . Mid way is (1/2+0)/2 = 1/4
Then returns to Office. Midway is (1/4+1)/2 = 5/8
Then returns to Home. Midway is (5/8+0)/2 = 5/16
Again To Office Midway will be (5/16+1)/2 = 21/32..
SO on and so forth!
no! that is the thing it seems like.. isnt it :)
but just imagine if he is at 1/2 and the next position is towards the office, he will reach (1/2+1)/2 =3/4
and if the next is towards home, he will reach (1/2+0)/2 = 1/4
so definitely it will not be a limiting case?
Yes good work Celestine :)
This is a very Famous question called the Vacillating Mathematician's problem. The interesting thing about the limit here is that it is not a single point. The first conclusion seems to be that he will reach the center! but that, as u can see is not the right solution!
Btw i have edited ur post to hide the correct solution!
dear nishant
when u edit to hide an ans
it becomes visible when one selects part using cursor
Hahah.
yes Celestine .. that is the basic idea..
so that it becomes visible to those who want it to be visible! :)
One can use the hide link when u want to give hints etc :)
taking home towards office as positive and backwards as negative...
wat the man actaully does is...
his displacement : +1/2 - 1/4 + 3/8 - 5/16 + 11/32 - ......
== (2-1)/2 - (21-20)/22 + (22-(21-20))/23 +.....
general term is : (-1)k-1[2k-1 - 2k-2 + .... +2k-(k-1) - 2k-k]/2k
= (-1)k-12k[1/2 -1/4 +1/8 - 1/16 +..... +1/2k-1 + 1/2k]/2k
=(-1)k-1[1/2((-1/2)k-1)/(-1/2-1)]
for k->infinity, the above expression tends to (-1^(k-1))/3.....
so position of the man afetr infinity time,,, x=1/3 or 2/3.
correct me, if wrong.......
Yes sky.. wonderful solution :)
Good work..
Now what will be his position at t tending to infinity!
I mean what will happen when it tends to infinity ?
There is slightly more to it indraneel :)
2/3 and a bit more.. and then a slight explanation of it
but it is good that u reached so far :) well done
So sky's solution above gives clearly that there are two points one at 1/3 and another at 2/3
So we need to understand what happens.
he basically reaches 1/3 then moves back towards office. Then returns from 2/3 which is midway between 1/3 and 1. Again he moves back from 2/3 to 0. the midway of this is 1/3.
So he keeps oscillating (Vacillating) between these two points. Hence this problem get its name "Vacillating Mathematician"
It is a special case of limits which shows that simple looking situations may not lead to a point limit. but to two point limits.
According to the definition of limits that we know, It will give "Limit does not exist". But just to give a feeel. this is what is happening here. I hope u guys could get some feel good by knowing this problem. I know this wont help u directly in IIT. But that this inspires u to like mathematics! :)