k i understand
im only telling that rθφ is sort of wrong approach
To be fair, this question is not relevant to the Syllabus of IIT JEE.
It is definitely in the syllabus but it shows how things can go wrong!
I will try to show that there are 3 different probabilities attached to finding the length of the chord of the circle which are of lenght greater than the side of the equilateral traingle inscribed in it
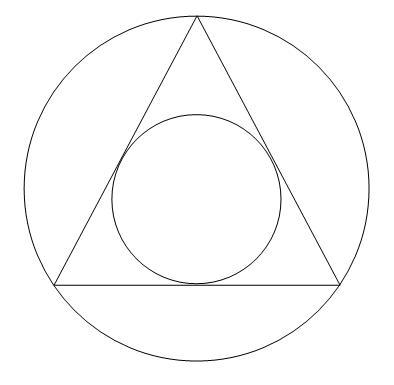
Here the outermost triangle and circle inscribed in it
Hahah.. you wont..
That is why my Question started with "To be fair, this question is not relevant to the Syllabus of IIT JEE."
I really wanted to give this question because this is one of those questions that really inspire a lot of ppl into mathematics and I am hoping that a few of you start to love Mathematics after seeeing this proof. That is all :)
cheers...
There is a n explanation to why all these are correct.. I will give taht today or post a link to it :)
THIS IS SUCH A TRAGIC PROOF!!!!!!!
ALL THREE SEEM TO BE PERFECTLY LOGICAL......
MAYB IF SUM1 WER 2 CRACK THIS PARADOX IN THE 22ND CENTURY IT WUD BE PROVING/DISCUSSING THE UNIFORMITY OF LINES as sir suggested..... [3] [4]
THIS IS JUS AMAZING!!!!!!! [1]
k i understand
im only telling that rθφ is sort of wrong approach
celestine i know where u are getting confused...
You cannot say that infinity and infinity is the same. I agree to what you are saying.. but the problem is that it is your way of looking
wee have in our life seen things in xyz coordinates nto in rθφ or some toher coordinate system. I know this is demanding too much right now.. but you have to be able to get away the bias for why xyz have to be uniform and not r, theta!
sir i can prove that lines cant be dist uniformly across circumference
consider thin rod of lenght l rotating at l/3 for angle θ
let n lines be created uniformly
now in one end thes n points occupy lθ/3 units in the other end they occupy 2lθ/3
contradicts uniform distribution .
wat do u say
cos only points filing circle will cover entire circle
in first two cases even with infinite lines and curves its impossible to cover entire circle
celestine.. u are partly right.. but din u take that as an assumption??
Where was that part given..
there are too many points in the space... we cant be that sure after all ;)
yes i was saying that only in my previus posts regardinh the distribution
in reality points are distributed uniformly in circle
This might be a bit tough to understand.. when i heard this it took me full 2 days to digest what was going on.
See what happens is that in the case 1 we are assuming that the points are distributed unifomly along the circumference.
In case 2 we are assuming that the lines are distributed uniformly on the plane
in case 3 we are assuming that points are distributed uniformly in the circle.
This is the basic reason.
We were not given initially what was the thing that was uniform!!
I donot guarantee (And I dont expect!) that everyone of u will understand what is going on. Even getting convinced is not that easy.
I hope there are atleast a few who can appreciate the difference!!!
It might have gone over the head of many many of you.
If you are not convinced. Let me know I will try to explain the reason more!!
ok i understand the problem is with assumption that a circle can be made out of superposition of infinte radial lines from centre .
this however is mathematically a wrong assumption as wen u increase no of lines to decrease space btw them the limit fluctuates depending on mode of distribution of lines
can u post ur explanation;)
No whne you are shifting the point, just shift the traingle as well
Case 1:
You are getting biased by the locaiton fo the triangle.
Just take that point anywhere and try with the set of lines originating at that point. The whole idea is that even in that case the probability will be 1/3 rd. Think about any point in between the two vertices. Apply the same logic threre. does the probability change? It does not! So the total probability will be the same.
Ditto arguement works with Case 2!
but then it wont be distibuted evenly only case 3 has even distribution of points
see in 1 wen u shift from one θ to another the in between space is unnoccupied
its definitely wrong
in 2 wat ur saying is wrt to a given set of chords think abt those who dont belong to that set
i definitely dont agree that all ans are correct
only 3 is correct explanation in terms of even distrubution it includes all chords in circle
Wel Celestine i can get a diff answer 4 d same question...........
wat is 100/200???
ans a. 10/20;
ans b. 5/10;
ans c. 1/2;
hehe
the above ques is also of same type i GUESS.......... d logic is d same but diff. approach......
No Celestine.. that is not the reason. I have the arguement.
See my post above Post no 13!
And it is not against nature. There is a reason why all these are correct!!
if its been there for 150 yrs then i think ive just solved it in my post up there
im very sure of my assertion im not confused;)
u cant get diff ans for same q its against nature
Proof 1: Take any chord from the vertex.. if it lies withing the middle of the triangle it will give a chord of length greater than the side of the triangle!
so probability = 60/180
so nishu bhaiyya, wat if v get this as a ques in one of those MCQs and all d three options are ther........wat shud v mark????????
more appropriate answer is............. since this is a very famous paradox.....and it also has a name.........my logic says tht this must be very special so i think all r right heheh...
Guys dont get confused...
All three are correct :D
Well the 2nd part you can take all the rotations and for each rotation there will be chords with the same probability. They are disjoint sets. Hence the net probability will be same!
So Celestine you pointed out a mistake.. good you thought that much.. But that is also correct!!
Option 1 is also correct!!!!!
it is by a slight modification of the logic for part 2!
"Dont try to find the mistake... try to see the brilliance" Cos there is no mistake!
This is a known paradox for 150+ years... ;)
w8.......i think all are right.......i cant see any fault in d first 2 either.......
wel...... even i think proof 3 is more correct.......but cud u explain hw did u get d prob. as 1/4??? i mean hw is d ratio of d areas 1/4???
celestine r u getting the same ans by this mid point method for the prob question .........do tell me ur ans plz .
proof 3 is only correct
a chord is uniquely defined by its midpt
in 2 we are restricting ourselfs to chords parallel to base
in 1 that prob satisfies by fixing one end
if its apllied to whole circle the prob wouldnt remain same as we will be reconsidering already considered chords
Proof 3: Any chord is fixed by its mid point! (why!!)
Now for any point that lies within this circle (smaller) will give a chord of lenght greater than the triangle's side
so the probability is area of smaller circle/ larger circle!!
=1/4
Which is something else (again easy to calculate!)
This problem is called the "Bertrand's Paradox" It is very famous. And Nothing that I have done.. Just that i got to know about it before you ;)
proof 2: Draw a chord parallel to the base.. If it lies above the base till the center it is of length greater than the side
So this will give a different length (easy to calculate :)
=sin(30) = 1/2