that answer was for the solid one ..
A Sphere of mass M and radius R is compressed to a disc..
The radius of the disc remains the same as R..
Mass also falls down to the same level. .(means there is no sideways movement of mass during compression)
What is the Moment of inertia of this disc..
(Trust me it is very easy.. )
Yesterday someone asked me this case :)
-
UP 0 DOWN 0 1 22

22 Answers
can anyone point out the err in sky's soln .. ? coz i cudn get anything out of rohan's method ....
celestine what will happen here is that the disc will have a different mass distributio nwith radius..
because the mass at the center will be higher than at the edge..
i am not able to understand the question and discussions
MOI of disc is MR2/2 always abt the standard axes
btw, final ans i got as 2/5MR2 instead of 1/5MR2.....
but wats the error in my process ?
i wanted to know here the mistake in my method bhaiya ........ [2]
no replies? [2]
for the hollow one ..
only difference
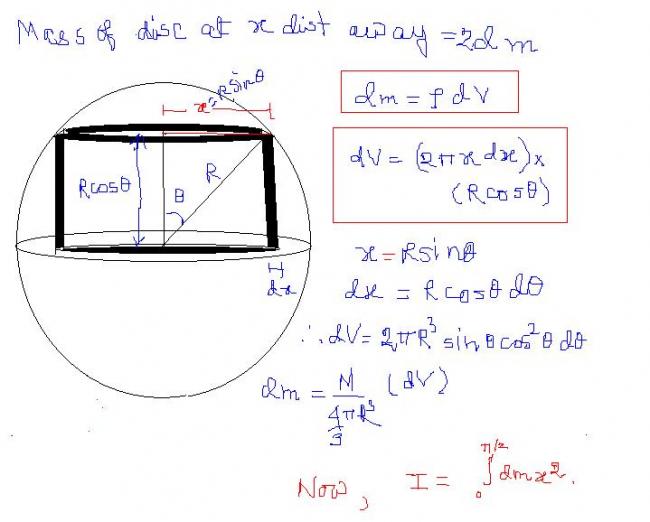
dM=Ï(2Ï€R2sinθdθ)
where cosθ=x/R
here is my method point out whether i have understood the problem clearly or not..
let us take the mass piece dM at a distance x and thickness dx
we have the mass of that part =
ÏÏ€(R2-x2)
further moi contribution due to that element = (let its length be L)
dML2/12 + dMx2
further we have
L=2√(R2-x2
we get
dI = dM(R2/3 - 2x2/3)
integrating from -R to R we get the answer ..
no tapan... I think you have not understood the question..
We are just pressing it.. Like if you have seen a "Foam" ball.. or the one which is very soft.. if you press it with your palm.. it will become like a disc..
Thus, what happens is that the disc gets formed..
Rohan is this the answer to the hollow one or the solid one?
So v consider mass density remains Konstant ne,....
\
Area down to pi R2 instead of earlier 4 pi R2
So v get mass factor reduction of 4
MOI Sphere : 2/3MR2 ............
MOI disc : 1/2(M/4)R2