Final answer?
Q.1 A ball B1 with mass(very small) m1 sits on the top of another ball B2 of mass m2. The bottom of B2 is at a height H above the ground and the bottom of B1 is at ht H+D above ground. Both ball are dropped from rest. All collisions are elastic. Find the height to which B1 rises.
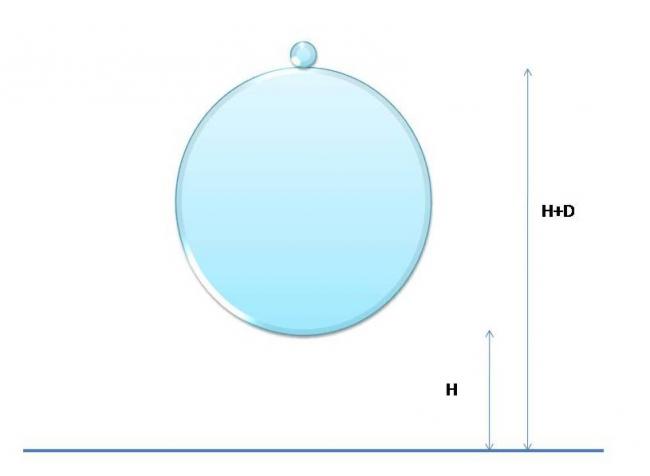
-
UP 0 DOWN 0 3 5

5 Answers
This is a famous ques
height=D+9H
soln..
before collison ,both move with √2gH=v
after B2 collides it satrts moving upwrd with v(becoz e=1)
but B1 stilll moves down with v
so vrelative=v-(-v)=2v
after the balls collide with each other,the basket balls speed remains same i.e v upward whereas relative velocity is 2v
so velocity of small ball after collison is in upward direction(becoz mass very small)=2v+v=3v
applying energy conservation
we get height rise=D+(9v2/2g)
but v2=2gH
=> h=D+9H