This is another good one about complex numbers. I am not trying to get a solution. I am sure many of you can.
I got this question from a user(Integrations) here. (I modified that one slightly!)
I want to stress the importance geometry can play in solving questions of Complex numbers. And why the importance of understanding Argand plane's equivalence with the XY plane of coordinate Geometry!
Find the locus of z such that
|z.k + 2i| > √2 for all real values of k
and that z is in the 4th quadrant.
Note: I have changed the language of the question to take away all the complexities.. so that you get a much simpler thought process :) I hope this hleps.
9now the q is much more simpler its upper half of 4th coordinate cos x+y = 0 is tangent upto which it can reach
ive explained that already way beeeeefore in my prev post . i think that was correct for earlier q u gave
62Yes rohan.. but can u think of something much more elegant??
think graphs :)
1i just saw and posted ... :D
didnt think of anything else ...
:)
ya i think graphs will make it better :))
1hmm by geometry i think let the length of z.k be x ... in the fourth quadrant
the question demands that if we go on increasing / decreasing the length in the direction of z
the resultant of vectors 2j^ and z.k will have magnitude >√2
let the angle between 2j^ and z be θ
then
|resultant|>√2
4+x2+4xcosθ>2
for all values of x if cos θ would be fixed ..
as x is in third quadrant x=-p
hmm. getting the same solution with almost same method
62this is not pure geometry...
could you think something much more brilliant... That you start to pat your back once you solve it ;)
1yikes ive taken for 3rd quad........... EDITING.......
wel.........is this right......... let z=x-iy...
so mod(zk+2i)>√2...
that is mod((x-iy)k+2i)>√2
that is mod(xk+i(2-ky))>√2
that is √((xk)2+(2-ky)2)>√2
that is (xk)2+4+(yk)2-4yk>2
that is x2+y2-4y/k+2/k2>0
which is the exterior of a circle.............
..................DONE EDITING............
1i still dint understand................. x2+y2-4y/k+2/k2>0
is a circle for all real values of k rite?????????
1wel if v hav any prob lets differentiate it.......
so
2x+2ydy/dx-4/kdydx>0
so.......dy/dx(2y-4/k)>-2x
1and dy/dx=x/(4/k-y) which is.....
dy/dx=(xk)/(4-yk).....................so wat????
1hmm
let us fix one point (q,-p) belonging to z
then it follows the condition
|(q-ip)k + 2i|>√2
in other form
(-pk+2)2+(qk)2 >2
we get
p2k2+4-4pk+q2k2>2
(p2+q2)k2-4pk+2>0
as we have fixed (-p and -q) , the above relation must hold for all k
that is the minimum value of this expression must be >0 and further to have a minimum
f''(k)>0 which is true
we get minimum value as
2 - 4p2/(p2+q2)
hence we get
2q2>2p2
or
(q-p)(q+p)>0
but q+p>0 (as both +ve)
hence q>p
or
x>-y
x+y>0
hence,
we get that portion in the fourth quadrant where x+y>0
62How about this....
kz will give a line passing through 0 and z (when k goes through all the reals)
Now this is a line!
we want that |kz+2i|>√2 for all k
so we want that the distance of this line from -2i be more than √2
so distance of a line through origin from the point (0,-2) should be more than √2!
The limiting case is this. The arrow starting from (0,-2) gives the perpendicular line. Its length here is √2 (for the limiting case!) for other casees it will be more
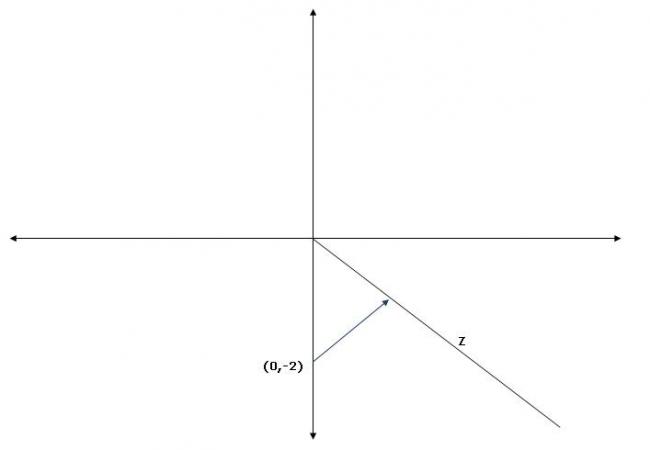
So the final solution will be the points which are above the strraight line and below the x axis.
9and that line ur saying is x+y=0 i think rohan also got that
62yup i did say Rohan is correct :)
I only wanted to show how this complex looking problem can be solved with such simplicity!
33What i did....
Wrote the given as |z+2i/k|>√2/k ............. for k>0 ;)
Now it represent z as area outside circle having center at -2i/k and radius √2/k for different k.....
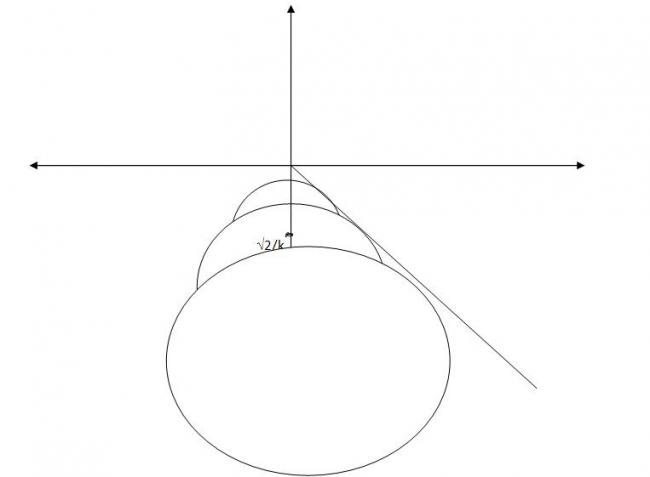
Also notice that distance of x±y=0 from -2i/k is √2/k.....
Hence the answer..... on the right side of line x+y=0 as it is outside every circle....
33@ Akand.......
u got ;
x2+(y-2/k)2>2/k...
Right...
Then think of its center and radius...
33on this conclusion u could have reached by complex no also see my earlier post(2 post up)...
From this onward reasoning is same what i gave..
here center and radius is not fixed...
so actually its exterior of circles for different k so its union will give the answer...
33Seen my fig above... and the two lines below it and let me know if its clear..
actually x+y=0 will cover the circles completely like a envelope from right and region towards its right is the req region
62maddy, celestine... u guys are taking "K" .. there is one k in the question!
62i modified that question.. i messed a small thing.. :(
that made the question too stupid..
there was a mistake in ur solution even then.. (what about k?)
1oh shit! harbari me garbari :(
i left the coeff of x^2 and y^2 intact..