Yes Satan, you have done a wonderful job..:)
And Priyam, I actually was looking for whether somebody comes up with the solution you have posted(only it will be parallel axis and not perpendicular axis theorem as you say). This is a much slicker way to find the required moment of inertia. You just have to notice that the each smaller unit is exactly similar to the final object.
Now that the idea is out in the open, try the next one which I have posted.
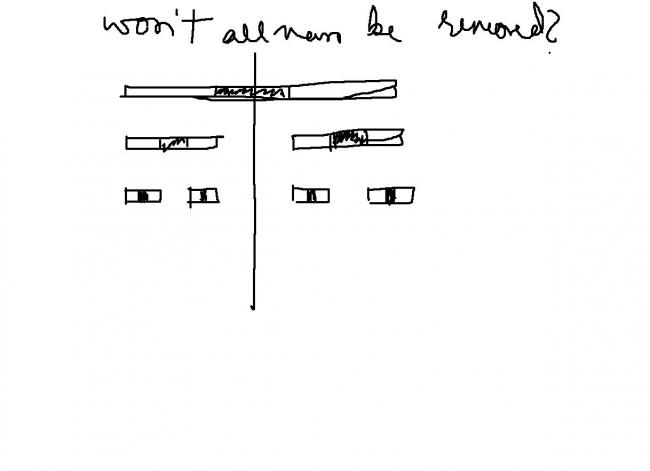
Take a (one-dimensional !) rod of length \ell and remove the middle one-third. Then remove the middle one-third of the remaining two pieces, then remove the middle one-third of the remaining four pieces, and so on forever. Let the mass of the final object be m. Find the moment of inertia of the final object about an axis through the center of the (original) rod and perpendicular to it.
-
UP 0 DOWN 0 5 29

29 Answers
Kaymant sir,
i loved this question and your integration question.
I am adding this one to the QOD. :)
Phew!!
I think i got a smaller method... (Big hint from Satan... U can say his modified solution..widout those n... thanx Satan...[1])
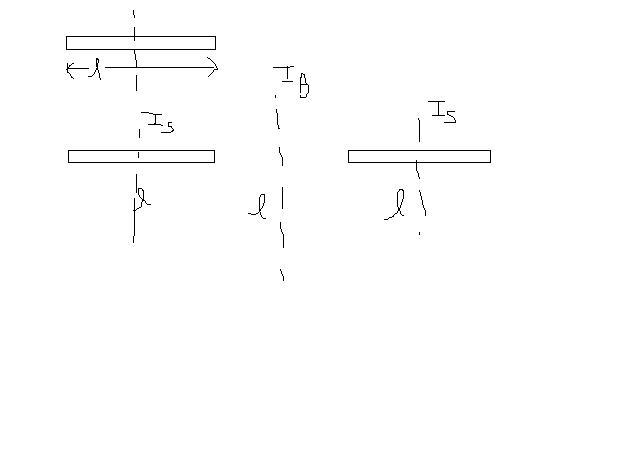
Is be moi of the given rod(structure.)
Now if two struct are put at a dist of l then it gives a new big struct of length 3L
I is proportional to L2 and m
L increases 3 times in Big one and m becomes twice...(two small structures..)
Is=KmL2 (thanx to satan..)
Ib=K(2m)(3L)2=18Is ..(i) ...Ib is moi of bigger structure..
Dist b/w Is and Ib axis=L/2+L/2=L
so by perpen axis pararllel axis theorem... second fig... .edited as told by Kaymant Sir..in post below..
Is+mL2+Is+mL2=Ib
2Is+2mL2=Ib..(ii)
From (i) and(ii)
Is=mL2/8
K in both Ib and Is is same since same structures only having diff dimesnions...
BOY O BOY!!!!!!
I M overwhelmed by the solutn!!!
simply awesome!!!
gr8 work SATAN........
Ok let me post the method too ..
first of all let us go to that situation where there has already been n turns of removal of parts then the number of pieces
= 2n mass of each piece = M/3 n total mass = M(2/3)n
further the moment of inertia of the whole thing about the line passing through the centre and perpendicular to the pieces =kML2
where k will depend on n
let us consider the case after n-1 divisions were carried out and after n divisions were carried out after the n-1th division was carried out
moi about centre=let kML2 where let M be the mass of each particle
after the nth division let us consider the moi about the com of the right part to the centre(at a distance of L/3 lies its com)
we see that it is a similar case to the earlier except the fact that all dimesions are 1/3rd so the moi =kM/3L/32=KML/27=In-1/27
further the mass of the right half=(2/3)nM/2
here M is the initial mass
so the contribution of right half to In=
In-1/27 + M/2(2/3)n(L/3)2
as its com lies at a distance of L/3 (as earlier mentioned)
the contribution from the left half will be same ..
so we get the relation In=2(In-1)/27 + (2/3)nML2/9
with I0 = ML2/12
solving this sequence we get the general term as
ML2(32n+1 - 1)(3-3n-1)(2n-3)
at n-> infinity this reduces to only ML2(2/3)n/8
but given final mass= m so M(2/3)n=m
we get answer as mL2/8
well its a good problem .. i hope i got the correct answer
well i got the answer as mL2/8 can i get a conformation
Koi trick to nahi dikh raha abhi... lekin my dimag is processing it![]()
:P
--edited--
finally my dimaag processed.. :D so i replied below...
--edited--
[12]
either this is turning out to be a maths question....
or there is something tricky that will make us feel stupid when the answer is given.......
I think some more guys should try this before the answer is given..
remove the middle one-third of the remaining two pieces
is equivalent to
removing one-third from the midle one-third.
let the last length remaining be x.
so
x= l - 2l/3 - 4l/9 - 8l/27 - ...............∞
=> x = l - l(2/3 + 4/9 + ....... ∞)
= l - l((2/3)/ (1 - 2/3)) = -l ??!#@$#!!!!!!!
This object is the so called Cantor set (or at least a mechanical analogue). It has no length, so the density of the remaining mass is infinite. If you suddenly develop an aversion to point masses with infinite density, simply imagine the above iteration being carried out only, say, a million times.
Okay to give you an idea of the process, here are the first two steps in the procedure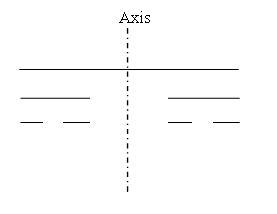
This process is repeated indefinitely.
\frac{1}{3} + \frac{2}{9} + \frac{4}{27} + \frac{8}{81} + ... = 1 seems logical to me
no i too thot that... i dun think dats the case..
firstly toh i did something soethimg and got -L !!
but that was a mistake...
won't the whole rod be removed?
\frac{1}{3} + \frac{2}{9} + \frac{4}{27} + \frac{8}{81} + ... = 1